Теория счастья. Проклятие режиссёра и проклятые принтеры

Стас Молотов07.09.2018

0 4 Время чтения: 9 мин.

Продолжаю знакомить читателей Хабра с главами из своей книжки «Теория счастья» с подзаголовком «Математические основы законов подлости». Это ещё не изданная научно-популярная книжка, очень неформально рассказывающая о том, как математика позволяет с новой степенью осознанности взглянуть на мир и жизнь людей. Она для тех кому интересна наука и для тех, кому интересна жизнь. А поскольку жизнь наша сложна и, по большому счёту, непредсказуема, упор в книжке делается, в основном, на теорию вероятностей и математическую статистику. Здесь не доказываются теоремы и не даются основы науки, это ни в коем случае не учебник, а то, что называется recreational science. Но именно такой почти игровой подход позволяет развить интуицию, скрасить яркими примерами лекции для студентов и, наконец, объяснить нематематикам и нашим детям, что же такого интересного мы нашли в своей сухой науке.

Опубликованные главы:

• Введение в мерфологию
• Закон арбузной корки и нормальность ненормальности
• Закон зебры и чужой очереди

Мы порассуждаем о цейтнотах, дедлайнах и о невовремя ломающихся принтерах.

Стратегия балбеса

Одним из самых простых процессов, требующих минимума дополнительных предположений, является пуассоновский поток. В предыдущей главе мы говорили о случайных процессах. Хорошими примерами могут быть удары капель дождя по крыше, поток частных автомобилей на дороге, сильные землетрясения и т.п. Напомню, что его можно реализовать, случайно распределяя известное количество независимых событий по временному интервалу.

Cкажем, в цепочке $\$ событие $B$ может случиться только после события $A$ и перед событием $C$ , хотя моменты в которые эти события произойдут пусть остаются случайными. А что мы получим, если события перестанут быть независимыми, а будут образовывать упорядоченную цепочку? Первое событие мы расположим в произвольной точке, второе тоже случайно, но обязательно позднее первого, третье — после второго и так далее. Посмотрим, как разместятся такие упорядоченные цепочки на ограниченном временном интервале. Рано или поздно, время для выполнения задач закончится и цепочка завершится. Для каждого следующего этапа будет оставаться всё меньше и меньше времени, так что к правой части интервала (перед дедлайном) должно наблюдаться заметное увеличение интенсивности процесса. На рисунке показан пример построенной таким образом цепочки из $5$ этапов работы, на которую было отпущено $10$ дней. Назовём построенный нами процесс стохастической цепочкой с дедлайном, а выбранную безалаберную стратегию выполнения работы стратегией балбеса.

Пример стохастической цепочки с дедлайном. В данном случае пять дел сделать удалось, можно ещё успеть сделать шестое, а на семь времени уже не хватит.

Пусть в распоряжении режиссёра и труппы имеется $n$ дней для постановки некоего действа. Сформулируем задачу, взяв в качестве испытуемого, скажем, театрального режиссёра. Какова вероятность не уложиться в срок, реализуя описанный нами процесс выполнения работ? Подготовка разбивается на $k$ последовательных репетиционных этапов, каждый из которых требует один день на выполнение. Если подготовка мероприятия требует вовлечения разных людей и различных производственных процессов, то возможны накладки, болезни или попросту хандра — все предпосылки к реализации нашей стохастической цепочки с дедлайном.

Вот что получается для $n=10$ : Для начала, я обратился к имитационному моделированию, чтобы выяснить, как распределяется длина цепочек, которые удаётся выполнить в ограниченный промежуток времени заданной длины, пользуясь стратегией балбеса.

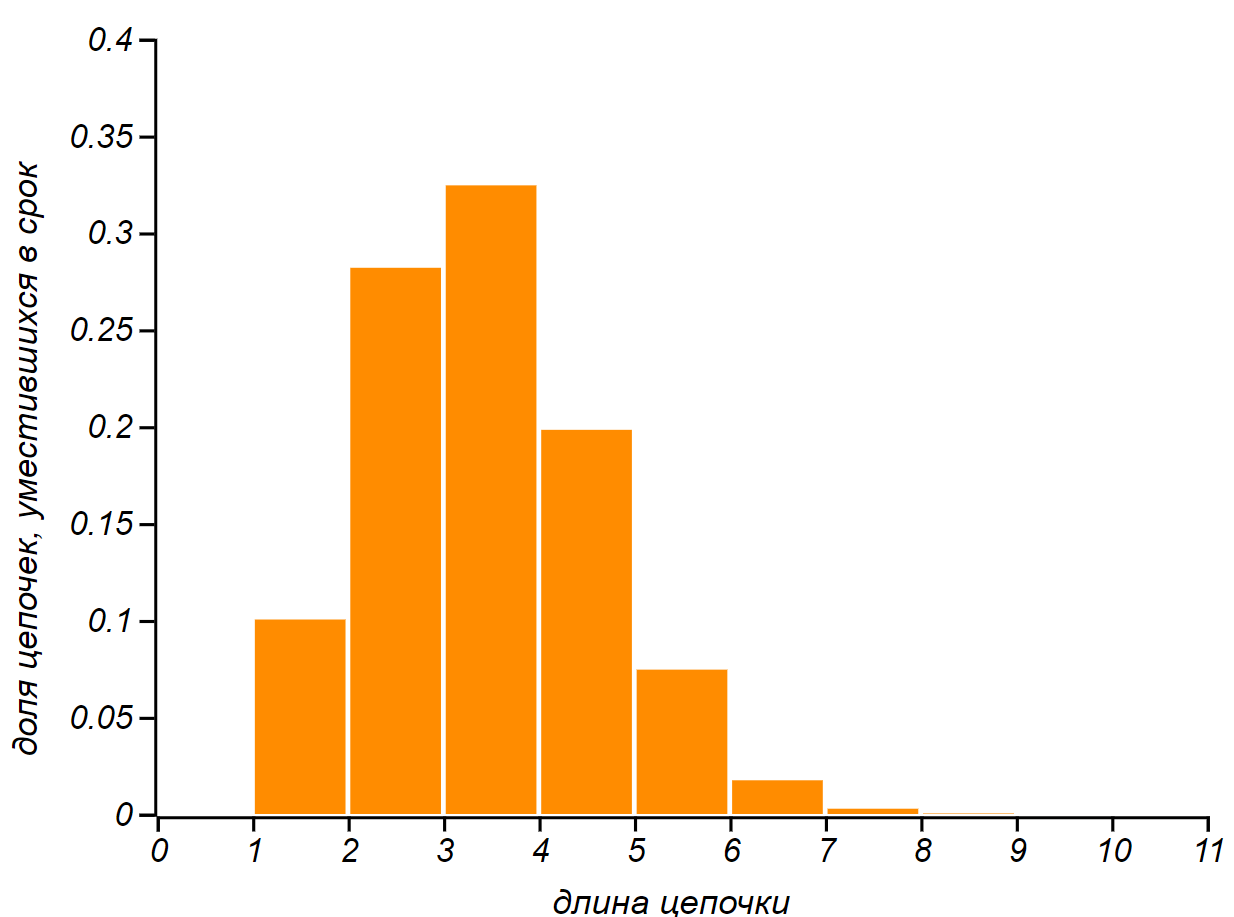
Функция вероятности для длины цепочек, которые удаётся сделать в отведённый срок.

Мне удалось получить аналитическое решение для функции вероятности в конечной форме:
Это распределение не встретилось ни в каких справочниках по теории вероятностей и математической статистике.

$P_n(k)=\genfrac{[}{]}{0pt}{}{n}{k}\frac{1}{n!},$

здесь $P_n(k)$ — вероятность выполнения цепочки длиной $k$ в $n$ отрезков времени, а конструкция $\genfrac{[}{]}{0pt}{}{n}{k}$ обозначает так называемые числа Стирлинга первого рода, они возникают в комбинаторике при подсчёте циклических перестановок. По праву первооткрывателя, назову это распределение именем Стирлинга. Удалось даже получить точные выражения для математического ожидания длины цепочек и их дисперсии:

$M[k] = H_{n},\quad D[k] = H_{n}-H_n^{(2)}.$

Здесь $H_{n}$ — это гармоническое число: частичная сумма расходящегося гармонического ряда $\{1,\frac12,\frac13,...,\frac1n\}$ , а $H_{n}^{(2)}$ — частичная сумма ряда $\{1,\frac14,\frac19,...,\frac1{n^2}\}$ . Собственно, ради вычисления этих значений я и исследовал получившееся распределение. Средняя длина цепочек с ростом $n$ растёт очень медленно, хоть и неограниченно. Не сильно ошибившись, можно сказать, что она растёт логарифмически. В свою очередь, дисперсия не сильно отличается от среднего, а добавочный коэффициент $H_{n}^{(2)}$ стремится к константе $\pi^2/6$ . Немного позже нам пригодится это наблюдение.

Видно, что шансов не успеть сделать одно дело нет совсем — для него время найдётся обязательно. Взглянем ещё раз на распределение длины цепочек. Доля очень длинных цепочек, ожидаемо, невелика и уменьшается с увеличением их длины, практически исчезая. Короткие цепочки из двух дел составляют десятую часть общего числа — это такие неудачные цепочки, которые начались в последний день (из десяти) и не оставили времени на продолжение. Ну, а цепочку из десяти дел случайно выполнить практически нереально — вероятность такого исхода равна $\frac{1}{10!}$ .

Построим такие кривые для $N = 7,\ 30,\ 365$ и $25000$ , соответствующие неделе, месяцу, году и (конечно, условно) всей жизни. На наш вопрос: какова вероятность, не уложиться в $n$ дней, имея перед собой $k$ последовательных этапов выполнения задачи, поможет ответить функция распределения — кумулятивная кривая для распределения Стирлинга.

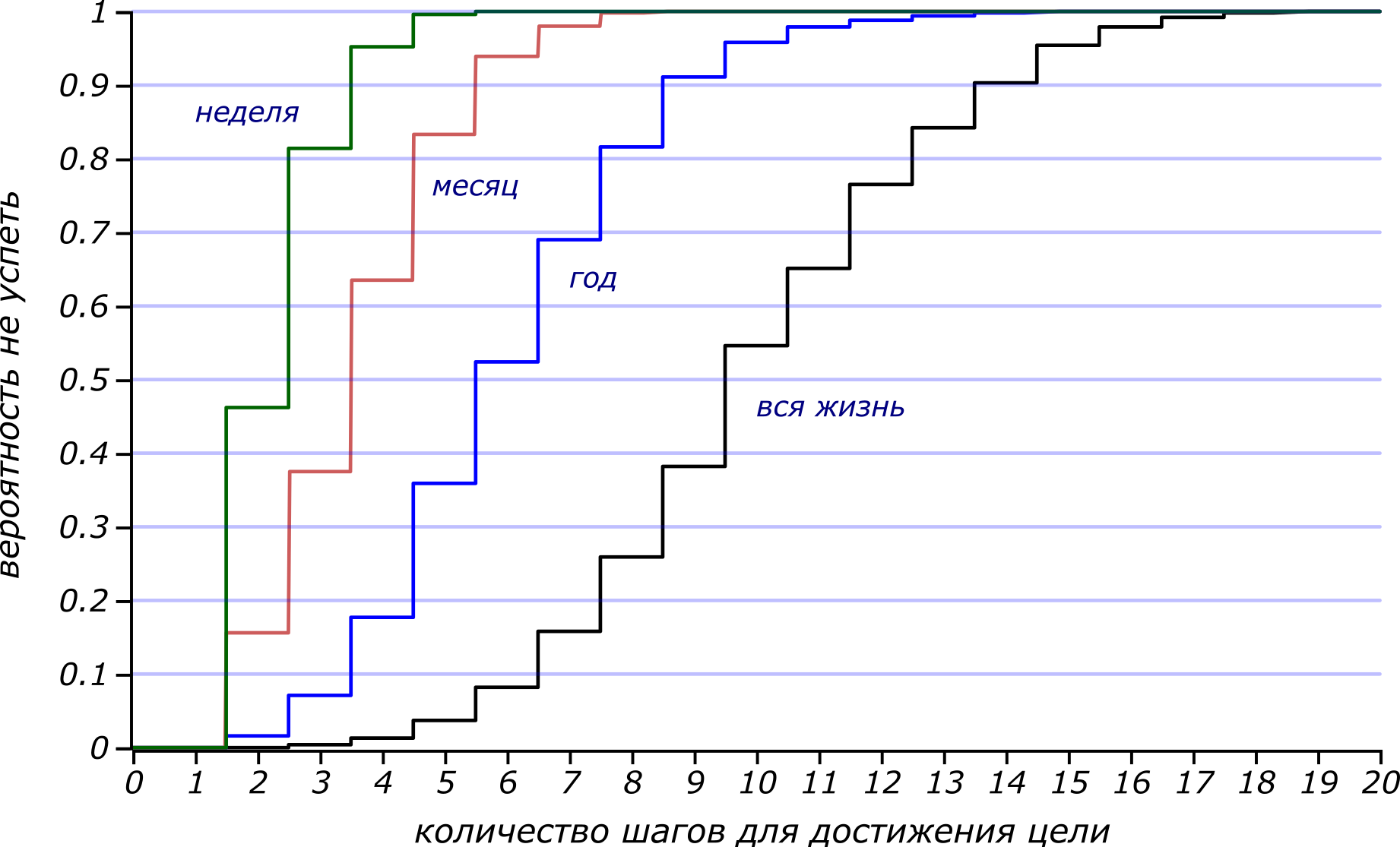
Вероятность не успеть выполнить цепочки различной длины в тот или иной срок.

И что неорганизованному балбесу в неделю лучше не планировать более трёх дел, а десяток дел он не сделает, с вероятностью, превышающей $50\%$ , и за всю жизнь! Эти графики говорят нам, например, о том, что вероятность не уложиться в месяц с заданием, имеющим $5$ шагов, превышает $80\%$ . Жизнь так коротка! Мы убеждаемся в том, что при увеличении сроков на несколько порядков, число выполнимых как попало дел увеличивается незначительно.

Быстрее, ещё быстрее!

Для этого построим несколько тысяч стохастических цепочек и усредним их, чтобы получить ожидаемый темп выполнения работы. Давайте теперь исследуем само явление цейтнота, его выматывающие свойства.

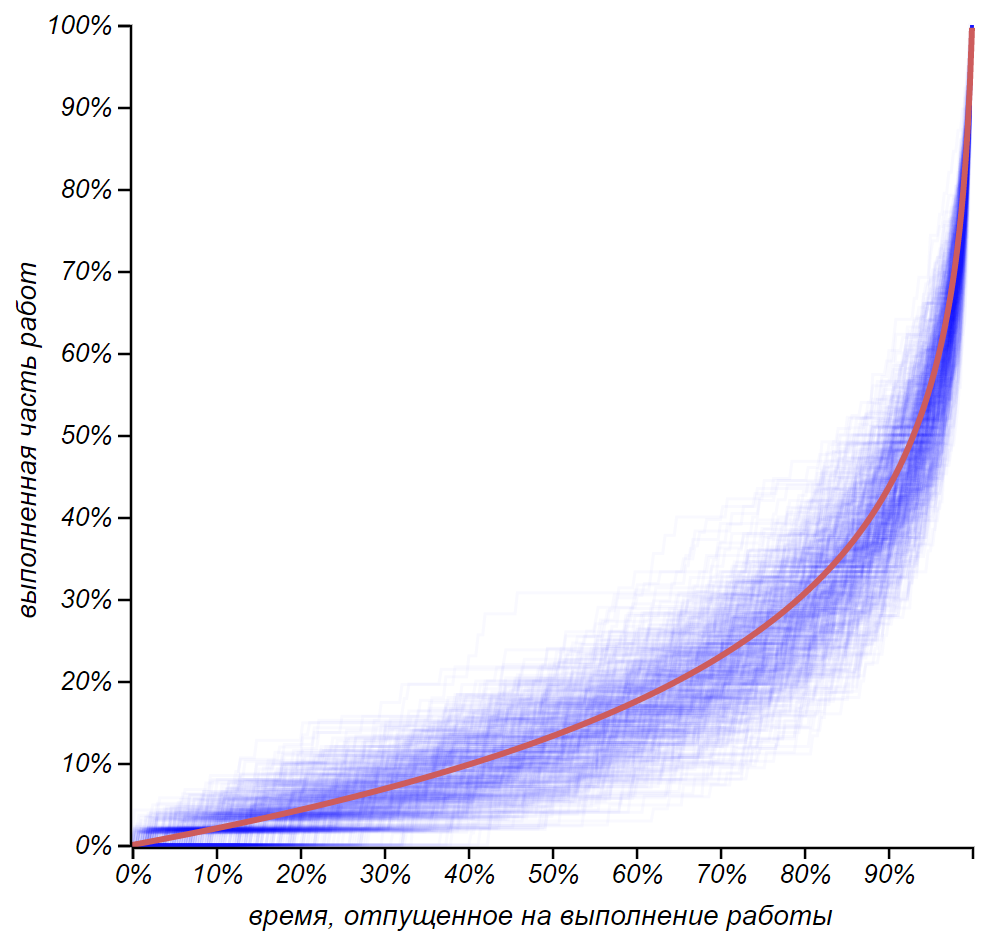
Множество стохастических цепочек с дедлайном и ожидаемый темп выполнения работы.

Это, с одной стороны, позволяет нам сравнивать, как разные сроки, так и различные по длине цепочки, а с другой — мы опять получили что-то подобное кривой Лоренца: некое формализованное отражение несправедливости. Обратите внимание на то, что оси графика приведены к общему числу дел и всему отпущенному времени.

Мы получили модель предновогоднего ража или паники в преддверии годового отчёта, а также нащупали закон подлости, знакомый всякому, кому приходилось организовывать концерт, костюмированный вечер или иное мероприятие: Наблюдаемый темп, увы, сильно неравномерен: в первую половину срока будет сделано едва ли $10\%$ работы, а добрую половину всех дел придётся выполнять, имея в своём распоряжении мене $10\%$ времени, но главная особенность: темп, вернее его наклон, стремительно увеличивается при приближении к дедлайну!

Сколько бы времени ни было отпущено на подготовку мероприятия, большая часть дел останется на последнюю ночь!

Неужели причина этого проклятия только в нашей неорганизованности и безалаберности? Прекрасные живые примеры таких процессов описаны, например, в рассказах Карела Чапека «Как делают газету» и «Как ставится пьеса». Стратегия балбеса, конечно выглядит глупо, но экспоненциальный рост темпа — это не шутки! Это, конечно основные причины, но мы не настолько в ней виноваты, чтобы нельзя было попробовать оправдаться каким-либо математическим законом. Можно ли вообще с ним справиться?

Формула не слишком изящна, однако примечательно, что в неё входит число дней $n$ и не входит число запланированных дел: Ожидаемый темп выполнения работы можно вычислить точно.

$T_n(x)=-\frac{\log_2\left[1-x \left(1-2^{-H_n-1}\right)\right]}{H_n+1}.$

Логарифм — функция медленная, если только его не прижать к стенке. В последние дни перед дедлайном темп растёт катастрофически, с такой же скоростью, с которой логарифм проваливается в бездну при приближении к нулю. Однако, от числа выделенных дней он, всё же зависит. Можно посмотреть на то как выглядит ожидаемый темп для недели, месяца, и года:

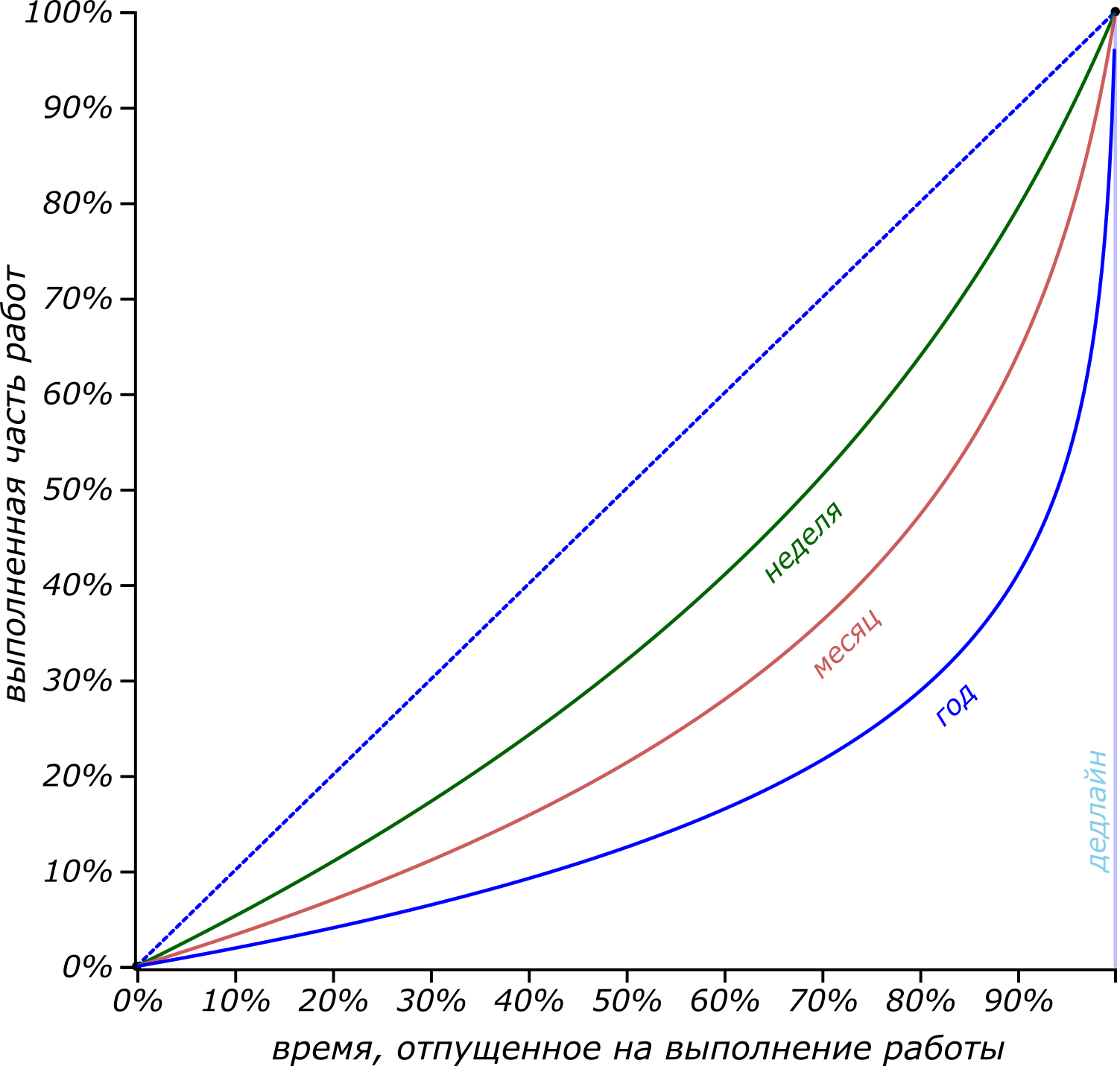
Наиболее вероятный темп выполнения работы в ограниченный срок. Интересно, что жёсткое ограничение по времени влияет благотворно. Имя в запасе всего неделю, мы, скорее всего, станем выполнять работу равномернее (к половине срока будет готова треть работы), а если впереди целый год, то можно и расслабиться, ну, а потом об этом пожалеть.

Это похоже на кривую равенства на диаграмме Лоренца, знаменующую справедливость. У идеального исполнителя-перфекциониста, который выполняет работу абсолютно равномерно, темп выполнения должен стремиться к диагонали (синяя пунктирная линия на рисунке). Он зависит от длины выделенного срока и потихоньку увеличивается с ростом $n$ . Подобно тому как мы вычисляли коэффициент Джини для диаграммы Лоренца, мы можем, основываясь на площади между кривой темпа выполнения работ и идеальной кривой, вычислить некий коэффициент подлости, который покажет насколько мы далеки от идеала. 25$" data-tex="inline"/>, <img src="https://habrastorage.org/getpro/habr/formulas/e78/df0/f11/e78df0f117fba4c311469dd145112d8f.svg" alt="$0. В приведённых нами примерах для недели, месяца и года, коэффициент подлости равен, соответственно $0. 65$ . 44$" data-tex="inline"/> и <img src="https://habrastorage.org/getpro/habr/formulas/bb0/873/f35/bb0873f35d8136573e2fa2028bae4d60.svg" alt="$0.

Можно, например, взять себя в руки. Как же бороться с нарастающей волной забот и цейтнотом? Правдоподобной моделью будет выбор момента для выполнения следующего дела, следуя экспоненциальному распределению с плотностью обратно пропорциональной оставшемуся времени. Человек с синдромом отличника может стремиться сделать следующее дело как можно раньше, насколько это возможно, конечно. Назовём эту стратегию стратегией благих намерений. Это не исключит некоторой неопределённости, присущей нашей жизни, но выразит благие стремления делать все дела как можно скорее. Вот какими будут распределения вероятностей выполнения заданий в срок для приверженца этой стратегии, который в половине случаев сделает очередное дело в первую четверть оставшегося времени:

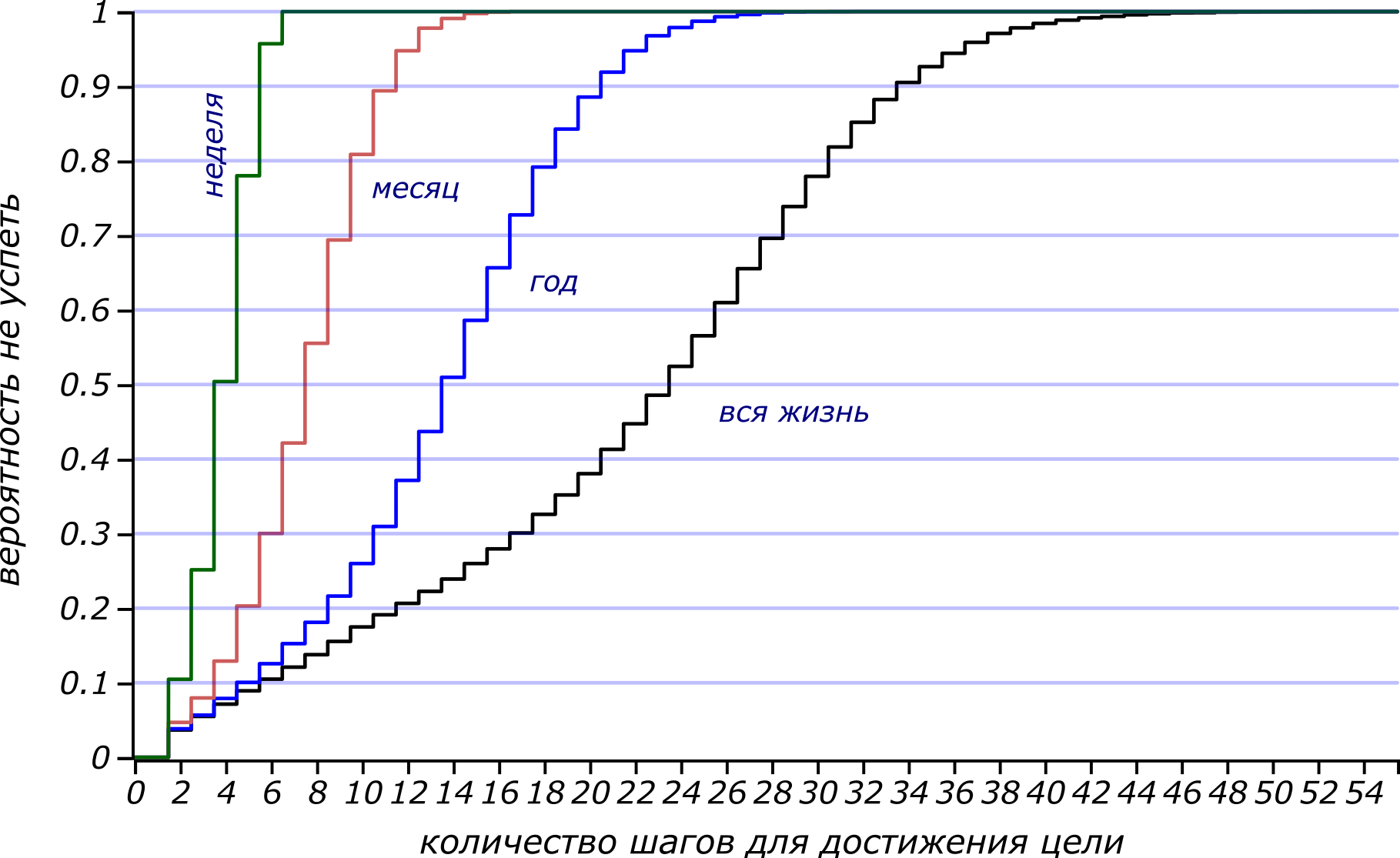
Распределение вероятности не успеть в срок для стратегии благих намерений.

В течение недели можно с неплохой вероятностью успеть сделать пять дел и оставить себе два выходных дня. Существенно лучше! Проблема кроется в том, что ожидаемое число успешно завершаемых дел всё равно остаётся пропорциональным логарифму отпущенного времени, а логарифм растёт чрезвычайно медленно! Но всё-же, для больших периодов увеличение возможностей не революционное. В любом случае, необходимо помнить, что жизнь коротка и чтобы успеть реализовать задуманное, нужно действовать прямо сейчас! Так что, планируя многое, нужно иметь в виду, что интенсивность процесса будет неизбежно возрастать, и времени в преддверии дедлайна, скорее всего, будет не хватать.

Давайте полюбуемся на темп благонамеренного отличника.

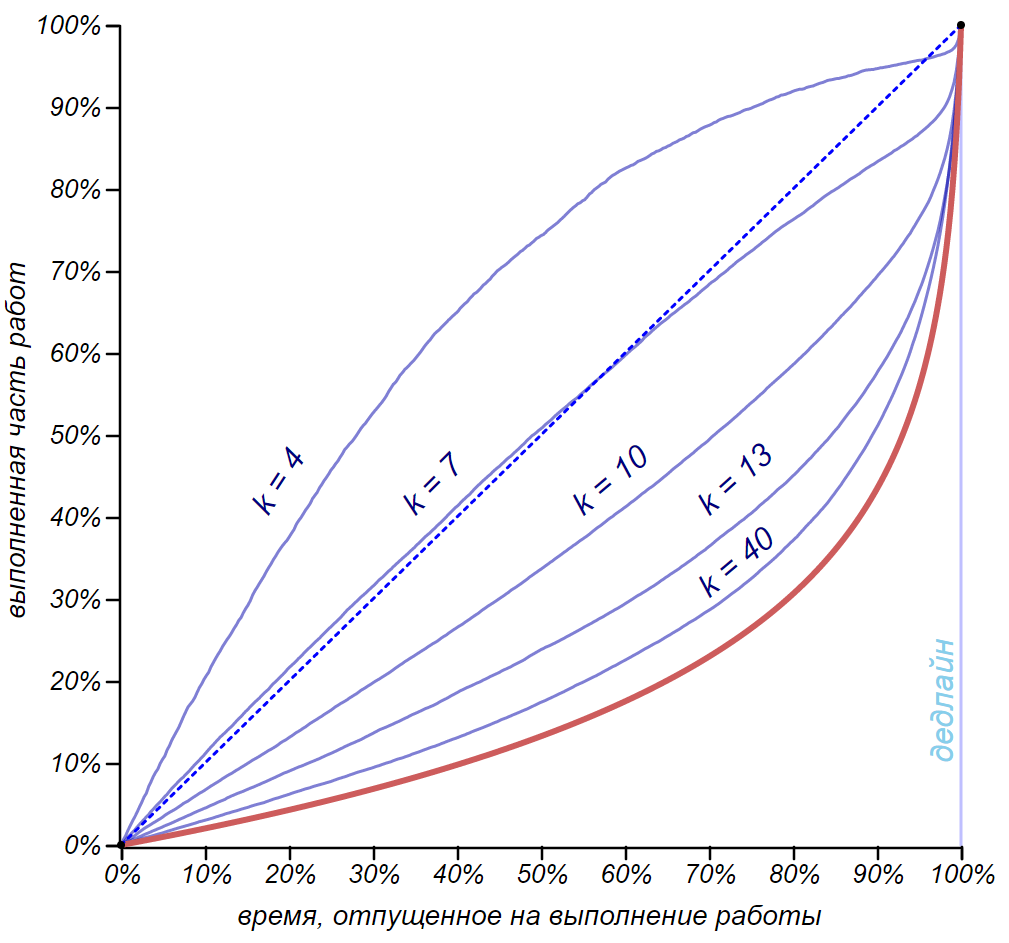
Ожидаемый темп выполнения работы методичным человеком, старающимся приступить к следующему этапу работы как можно скорее. На графиках представлены результаты усреднения десятка тысяч численных экспериментов, моделирующих выполнение задания с фиксированным числом этапов. Красной линией обозначен предельный темп для большого числа задач.

Короткие цепочки такой человек будет выполнять с существенным перевыполнением плана, а цепочку из семи дел — практически идеально. Нашему аккуратисту удалось более равномерно распределить работу, и сделать существенно больше дел, но его всё равно ожидает цейтнот. Увеличилась общая производительность, но запарка перед самым дедлайном никуда не делись. Однако по мере увеличения числа дел, ожидаемый темп быстро стремится к теоретическому темпу, полученному с помощью стратегии балбеса! Так что нагружая можно доканать и заправского зануду!

Давайте разобьем срок выполнения работы на две равные части и будем придерживаться этого нового дедлайна, считая его, скажем, промежуточным отчётом. Впрочем, существует ещё один широко известный способ существенно дисциплинировать выполнение работ: вместо одного дедлайна надо сделать их много. Для каждой из этих частей мы можем построить кривую ожидаемого темпа выполнения работ, как показано на рисунке.

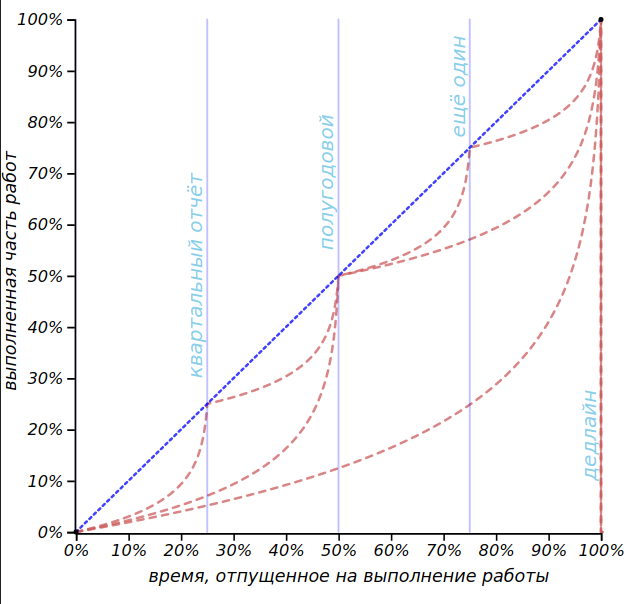
Разбиение времени выполнения работы на несколько промежуточных отчётных периодов позволяет выполнить работу более равномерно, но добавляет стресс при приближении каждого нового отчёта.

65$" data-tex="inline"/> до <img src="https://habrastorage.org/getpro/habr/formulas/34c/99c/5d3/34c99c5d3317cdd989bf0d0d03e51b22.svg" alt="$0. Несмотря на нервотрёпку с промежуточным отчётом, мы достигли свое цели: площадь под общей кривой темпа выполнения сократилась и коэффициент подлости уменьшился от $0. Кроме того, сокращение срока (вместе с сокращением числа дел, разумеется) приближает ожидаемый темп выполнения работы к идеальному, поэтому коэффициент подлости уменьшился более чем в два раза. 3$ . 13$" data-tex="inline"/>, но тем самым мы вгоним наших исполнителей сразу в четыре стрессовых периода и они всё равно станут громко страдать, жалуясь на судьбу и на начальство! Добавление ещё двух, скажем, квартальных отчётов, уменьшат его уже до <img src="https://habrastorage.org/getpro/habr/formulas/ac4/5bc/e4f/ac45bce4ff3f6cb5308cd460a35275e4.svg" alt="$0. Что же, мы можем показать работникам наши выкладки и доказать, что введя ежеквартальную отчётность, в пять раз понизили коэффициент подлости их жизни, если это, конечно, послужит им утешением.

Более того, при стремлении количества промежуточных дедлайнов к числу дней, отпущенных на работу, темп выполнения работы приблизится к идеальному, но очень занудному темпу.

Ну вот! Ещё и принтер сломался!

Полученное нами распределение показывает вероятность получить $k$ событий в заданном временном интервале. Добавим ещё пару слов о стратегии балбеса и распределении Стирлинга. Подсчитывая события в настоящем пуассоновском потоке с интенсивностью $\lambda$ мы придём к известному распределению Пуассона:

$P(k) = e^{-\lambda}\frac{\lambda^k}{k!},$

описывающее верятность получить $k$ событий в единичном интервале. Выражение для чисел Стирлинга имеет асимптотическое разложение, которое больших $n$ сводит распределение длин цепочек с дедлайном к смещёноому распределению Пуассона с интенсивностью $\lambda = H_n-1$ . Таким образом, наш стохастический процесс с дедлайном, с точки зрения статистики, можно рассматривать либо как пуассоновский процесс на сгущающейся временной сетке, либо как неоднородный пуассоновский процесс, интенсивность которого монотонно и стремительно растёт. И хотя, строго говоря, наш процесс не является пуассоновским, поскольку события в нём не независимы, однако, нужные нам статистические свойства у них схожи. Об их схожести говорит и подмеченная мной близость среднего значения и дисперсии распределения Стирлинга, характерная для пуассоновского распределения.

Этот вывод позволяет задать вопрос: что если добавить к построенному нами процессу выполнения цепочки дел какие-либо независящие от нас редкие неприятности: пургу, жуткую пробку, насморк, поломку принтера, или всенародный праздник?

Случайное прореживание с вероятностью $(1-p)$ оставляет процесс пуассоновским, но его интенсивность уменьшается, умножаясь на $p$ . Для пуассоновского процесса определён процесс случайного прореживания, заключающийся в том, что мы с какой-то вероятностью станем удалять события из потока. Так стремительно, что какой бы малой ни была вероятность неприятности, для достаточно большого числа дел (или срока, отведённого на работу), ближе к дедлайну она увеличится до вполне наблюдаемой. События, соответствующие совпадению неприятности и какого-либо этапа выполнения работы сами образуют пуассоновский процесс, с существенно меньшей интенсивностью, но в нашем случае, также, монотонно и стремительно растущей. И принтер забарахлит именно накануне сдачи курсовика!

Автобус не желает вам зла. Не удивляйтесь если автобус сломается именно тогда, когда вы уже опаздываете. И темп с которым вы летите навстречу судьбе уже такой сумасшедший, что начинают происходить самые маловероятные чудеса. Просто, если вы девушка, то последовательность дел: выбрать платье, съесть конфетку, умыться, надеть выбранное платье, накраситься, надеть цепочку, переложить вещи из сумочки в клатч, почистить туфли и прочее и прочее подходит к самому главному и волнительному дедлайну — к свиданию!

В конце концов, а что же такое чудо, как не реализация невероятного!

Теги