Сбалансированные двоичные деревья поиска: реализация на Julia

Лида Шиндлер02.08.2019

0 1 Время чтения: 19 мин.

Адельсон-Вельского и Е.М.
Иллюстрация из работы Г.М. Ландиса 1962 года

Широко применяются двоичные деревья поиска, в которых у каждого узла есть только два потомка. Деревья поиска — это структуры данных для упорядоченного хранения и простого поиска элементов. В этой статье рассмотрим два метода организации двоичных деревьев поиска: алгоритм Адельсон-Вельского и Ландиса (АВЛ-деревья) и ослабленные АВЛ-деревья (WAVL-деревья).

Двоичное дерево состоит из узлов, каждый узел хранит запись в виде пар ключ-значение (либо, в простом случае, только значений) и имеет не более двух потомков. Начнём с определений. Дополнительно в узлах может храниться (и обычно хранится) служебная информация — например, ссылка на родительский узел или другие данные. Узлы-потомки различаются на правый и левый, причём выполняется условие на упорядоченность ключей: ключ левого потомка не больше, а правого — не меньше, чем ключ родительского узла. Узлы, у которых оба потомка пустые, называются листьями дерева. Специальными случаями являются корневой узел, с которого происходит вход в дерево, и пустой узел, который не хранит никакой информации. Таким образом, каждый узел либо является корнем какого-то поддерева, либо листом. Узел со всеми потомками образует поддерево.

Будем считать, что пустой узел имеет специальное значение nothing типа Nothing. Это определение позволяет построить простейшую структуру для хранения узлов и самого дерева. Структура для хранения дерева содержит только ссылку на корневой узел. Тогда в узле достаточно хранить ссылки на правого и левого потомка и на родителя.

# K - тип ключей # V - тип хранимых значений mutable struct BSTNode key::K value::V left::Union{Nothing, BSTNode{K,V}} right::Union{Nothing, BSTNode{K,V}} parent::BSTNode{K,V} end mutable struct BST{K, V} root::BSTNode{K,V} end

Воспользуемся для этого подходом из книги "Алгоритмы: построение и анализ" и вставим в качестве точки входа в дерево не корень, а фиктивный узел, который будет своим собственным родителем. В этом случае возникает вопрос, каким образом представить пустое дерево. Для создания такого узла нужно добавить в описание структуры BSTNode конструкторы:

mutable struct BSTNode{K, V} key::K value::V left::Union{Nothing, BSTNode{K,V}} right::Union{Nothing, BSTNode{K,V}} parent::BSTNode{K,V} # пустой конструктор function BSTNode{K,V}() where {K,V} node = new{K,V}() node.parent = node node.left = node.right = nothing return node end # конструктор с парой ключ-значение function BSTNode{K,V}(key, value) where {K, V} node = new{K,V}() node.parent = node node.left = node.right = nothing node.key, node.value = key, value return node end end BSTNode() = BSTNode{Any, Any}() # Теперь структуру можно сделать неизменяемой! struct BST{K, V} entry::BSTNode{K,V} BST{K,V}() where {K,V} = new{K,V}(BSTNode{K,V}()) end BST() = BST{Any, Any}() Base.isempty(bst::BST) = bst.entry.left == nothing

ссылку на точку входа менять уже не потребуется. В этом случае структуру BST можно сделать неизменяемой, т.к. Далее будем считать, что корневой узел дерева является сразу и правым, и левым потомком входного узла.

Поскольку ключ левого потомка не больше, а правого — не меньше родительского ключа, процедура поиска элемента пишется очень просто: начиная с корня дерева, сравниваем входной ключ с ключом текущего узла; если ключи совпали — возвращаем значение, в противном случае переходим к левому или правому поддереву, в зависимости от порядка ключей. Главная операция, для которой нужны деревья поиска — это, естественно, поиск элементов. Если при этом дошли до пустого узла — ключа в дереве нет, бросаем исключение.

# Перегрузка функции Base.getindex() позволяет в дальнейшем # обращаться к элементу через синтаксис tree[key] function Base.getindex(bst::BST{K,V}, key) where {K,V} key = convert(K, key) node = bst.entry.left while node != nothing key == node.key && return node.value node = (key < node.key ? node.left : node.right) end throw(KeyError(key)) end

максимальное расстояние от корня до листа. Поиск элемента по ключу, очевидно, занимает время O(h), где h — высота дерева, т.е. все узлы, кроме, может быть, самого крайнего слоя, имеют обоих потомков. Как легко посчитать, двоичное дерево высоты h может как максимум содержать 2h+1-1 узлов, если оно плотно заполнено, т.е. Это даёт весьма оптимистичную асимптотику поиска элемента в дереве при его оптимальном построении за время O(log2N), где N — число элементов. К тому же понятно, что любую наперёд заданную последовательность ключей можно привести к такому плотному дереву.

Напишем наивную реализацию вставки элемента по ключу: Естественно, алгоритм добавления элемента в дерево поиска нужно строить таким образом, чтобы условие на порядок ключей выполнялся.

# Перегрузка функции Base.setindex!() позволяет в дальнейшем # добавлять или менять элементы через синтаксис tree[key] = value function Base.setindex!(bst::BST{K,V}, val::SV, key::SK) where {K, V} key, value = convert(K, key), convert(V, val) parent = bst.entry.left # отдельный случай - вставка в пустое дерево if parent == nothing newnode.parent = bst.entry bst.entry.left = bst.entry.right = newnode return val end key_found = false while !key_found if key < parent.key if parent.left == nothing parent.left = BSTNode{K,V}(key, value) parent.left.parent = parent key_found = true else parent = parent.left end elseif key > parent.key if parent.right == nothing parent.right = BSTNode{K,V}(key, value) newnode.parent = parent key_found = true else parent = parent.right end else key_found = true parent.value = value end end return val end

В наихудшем случае, если поступающие ключи строго упорядочены (хоть по возрастанию, хоть по убыванию), наивное построение дерева будет отправлять новые элементы всё время в одну сторону, собирая, по сути, линейный список. К сожалению, наивное построение дерева даст нужную структуру только на случайных входных данных, а в реальности они часто довольно сильно структурированы. Как нетрудно догадаться, что вставка элементов, что поиск будут при такой структуре происходить за время O(N), что сводит на нет все усилия по построению сложной структуры данных.

выравнивать высоту правого и левого поддерева у каждого узла. Вывод: дерево поиска при построении нужно балансировать, т.е. Простейший — задать некоторое число операций вставки или удаления, после которого будет производиться перебалансировка дерева. К балансировке есть несколько подходов. Другой же вариант — строить алгоритмы вставки и удаления сразу так, чтобы дерево постоянно оставалось сбалансированным, что даёт для любой операции гарантированную временную сложность O(log2N). В таком случае дерево будет перед балансировкой будет в довольно "запущенном" состоянии, из-за чего балансировка будет занимать время порядка O(N) в худшем случае, зато последующие операции до некоторого порога вставок/удалений будут выполняться за логарифмическое время.

Для некоторых реализаций операций с двоичными деревьями поиска сложность вставки и удаления O(log2N) является гарантированной, для некоторых — амортизированной, с ухудшением до O(N). В связи с тем, что есть алгоритмы, в которых дереву позволяют "разбалтываться", но после этого довольно долго операции можно проводить за логарифмическое время, прежде чем придётся долго приводить дерево обратно в сбалансированное состояние, различают гарантированное и амортизированное время вставки/удаления элемента.

Алгоритм Адельсон-Вельского и Ландиса (АВЛ)

В современной литературе по начальным буквам фамилий эта структура называется АВЛ-деревья. Первая реализация самобалансирующегося двоичного дерева поиска была предложена в 1962 году Адельсоном-Вельским и Ландисом. Структура описывается следующими свойствами:

Упорядоченность: для любого узла ключ в вершине левого поддерева меньше, а в вершине правого поддерева — больше, чем ключ самого узла (если потомки не являются пустыми узлами).
Возрастание высоты: высота родительского узла на единицу больше максимальной высоты его потомков. Высота пустых узлов может считаться равной нулю.
АВЛ-сбалансированность: для любого узла высоты правого и левого поддерева отличаются не больше чем на 1.

Чтобы условие АВЛ-сбалансированности сохранялось после каждой вставки, каждая вставка сопровождается операцией балансировки. Из этих свойств следует, что высота всего дерева составляет O(log2N), где N — число хранимых в дереве записей, а значит, поиск записи происходит за логарифмическое время. Для простоты, пусть там просто хранится высота узла. Для эффективного осуществления этой операции в каждом узле нужно хранить служебную информацию.

mutable struct AVLNode{K,V} # надеемся, что высота дерева не будет больше 255 # (не больше 10^38 записей) height::UInt8 key::K value::V left::Union{Nothing, AVLNode{K,V}} right::Union{Nothing, AVLNode{K,V}} parent::AVLNode{K,V} # пустой конструктор function AVLNode{K,V}() where {K,V} node = new{K,V}() node.height = 1 node.parent = node node.left = node.right = nothing return node end # конструктор с парой ключ-значение function AVLNode{K,V}(key::SK, value::SV) where {K, V, SK<:K, SV<:V} node = new{K,V}() node.height = 1 node.parent = node node.left = node.right = nothing node.key, node.value = key, value return node end end avlheight(node::Union{Nothing,AVLNode}) = node == nothing ? 0 : Int(node.height)

Вставка записи

Напишем обёртки для получения и замены дочерних узлов с использованием индексов -1 и 1 вместо левого и правого: Базовая вставка делается по стандартному алгоритму — спускаемся по дереву вниз, ищем, куда можно вставить новый узел и вставляем.

function child(root::AVLNode, side::Signed) if side == -1 root.left elseif side == 1 root.right else throw(ArgumentError("Expecting side=-1 to get the left child or side=1 to get the right child")) end end function insert_child!(root::AVLNode{K,V}, newnode::Union{Nothing,AVLNode{K,V}}, side::Signed) where {K,V} newnode == nothing || (newnode.parent = root) if side == -1 root.left = newnode elseif side == 1 root.right = newnode else throw(ArgumentError("Expecting side=-1 for inserting node to the left or side=1 for inserting to the right")) end end

Далее рассмотрим варианты, которые могут появиться (на рисунках зелёным обозначен узел, поменявший высоту, обрабатываемый узел — его родитель). Далее, идём вверх по дереву и ищем нарушения условий 2 и 3.

Случай 0
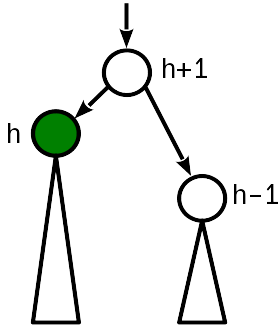
После вставки высота узла стала такой же, как у сестринского, и на 1 меньше (старой) высоты родительского узла.

Выше тоже уже можно не смотреть, т.к. Самый лучший случай, ничего дальше трогать не надо. там ничего не поменяется.

Вставка поднимает корень поддерева, и высота узла сравнивается с высотой родителя. Случай 1
До вставки высота узла была равна высоте сестринского узла.

При этом нужно продолжить двигаться к корню дерева, поскольку изменение высоты родительского узла могло привести к нарушению условия 2 на уровень выше. В этом случае достаточно "поднять" родительский узел, увеличив его высоту на 1.

Код

fucntion promote!(nd::AVLNode, by::Integer=1) nd.height += by end fucntion demote!(nd::AVLNode, by::Integer=1) nd.height -= by end

Случай 2

После вставки разница высот с сестринским поддеревом стала 2, причём "вытолкнуло" вверх левое поддерево:

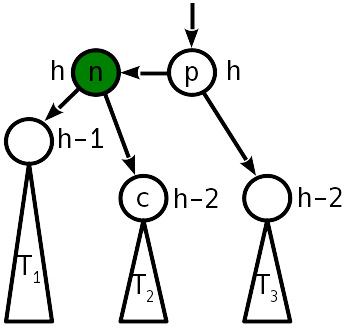
Проблема лечится операцией, называемой "простой поворот", преобразующей дерево следующим образом:

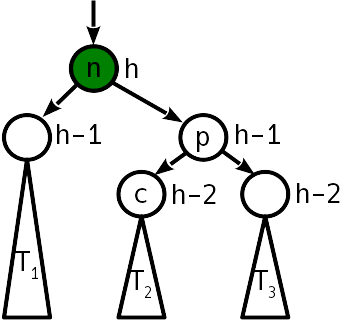
На простой поворот требуется 6 изменений указателей.

Это — выполнение условия упорядоченности. Обратите внимание, что в проекции на горизонтальную ось порядок вершин n, p и деревьев T1 — T3 до и после поворота остаётся одним и тем же. Как видно, после выполнения поворота выше по дереву балансировка уже не требуется.

Код

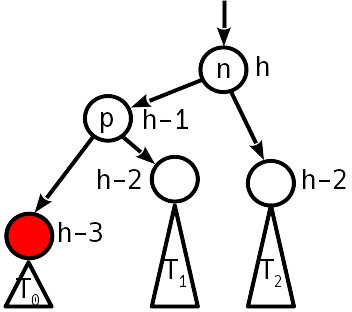
Случай 3
После вставки разница высот с сестринским поддеревом стала 2, причём "вытолкнуло" вверх правое поддерево:

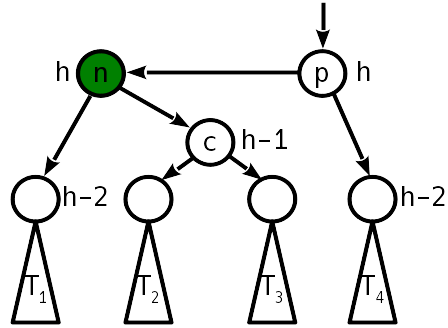
В этом случае одиночный простой поворот уже не поможет, но можно сделать простой поворот влево вокруг правого потомка, что приведёт ситуацию к случаю 2, который уже лечится простым поворотом вправо.

Тогда вместо 12 изменений указателей нужно будет только 10. Для уменьшения количества "перевешиваний" узлов можно два поворота скомпоновать в одну операцию, называемую большим, или двойным поворотом. В итоге двойного поворота дерево приобретает следующий вид:

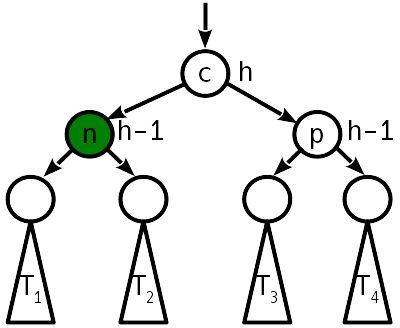
Как видно, после двойного поворота дальнейшей балансировки выше по дереву также не требуется.

Код

# pivot оказывается в конце на самом верху funсtion double_rotate!(pivot::AVLNode, dir::Signed) dir in (-1, 1) || throw(ArgumentError("Unknown rotation direction")) n = pivot.parent p = n.parent g = p.parent pivot.height = n.height n.height = p.height = pivot.height - 1 # "перецепляем" pivot к g pivot.parent = g g.left === p && (g.left = pivot) g.right === p && (g.right = pivot) t2, t3 = child(pivot, -dir), child(pivot, dir) # перецепляем n к pivot и t2 к n insert_child!(n, t2, dir) insert_child!(pivot, n, -dir) # перецепляем p к pivot и t3 к p insert_child!(p, t3, -dir) insert_child!(pivot, p, dir) pivot end

Объединим всё в одну функцию вставки. Итак, при вставке записи в АВЛ-дерево нужно O(log2N) изменений информации о высоте узлов и не более двух операций поворота. От базовой вставки она будет отличаться только тем, что после вставки нового узла вызывается функция fix_insertion!(), которая проходит от только что вставленного узла к корню, проверяет и при необходимости исправляет балансировку.

function Base.setindex!(avlt::AVLTree{K,V}, val, key) where {K,V} key, value = convert(K, key), convert(V, val) parent = avlt.entry.left # отдельный случай - вставка в пустое дерево if parent == nothing newnode = AVLNode{K,V}(key, value) newnode.parent = avlt.entry avlt.entry.left = avlt.entry.right = newnode return val end key_found = false while !key_found key_found = key == parent.key if key_found parent.value = value else side = (key > parent.key) * 2 - 1 # true == 1, false == 0 next = child(parent, side) if next == nothing newnode = AVLNode{K,V}(key, value) insert_child!(parent, newnode, side) fix_insertion!(newnode) key_found = true else parent = next end end end return val end

Если она равна 1 — мы находимся в случае 1, нужно поднять высоту узла и пройти выше. Функция fix_insertion!() проверяет разницу высот двух дочерних узлов, начиная с родительского узла от вставленного. Если она равна 2 — это случай 2 или 3, нужно применить соответствующий поворот, и дерево приходит к сбалансированному состоянию. Если она ноль — дерево сбалансировано.

# если правое поддерево выше - дисбаланс положительный, # если левое - отрицательный imbalance(node::AVLNode) = avlheight(node.right) - avlheight(node.left) function fix_insertion!(start::AVLNode) node = start.parent skew = imbalance(node) # у фиктивного входного узла дисбаланс 0 - т.е. попадание в него можно отдельно не проверять while abs(skew) == 1 node.height += 1 node = node.parent skew = imbalance(node) end @assert abs(skew) == 2 || skew == 0 if skew != 0 # повернуть надо в сторону более низкого дерева, # т.е. противоположно дисбалансу dir = -skew ÷ 2 n = child(node, -dir) prev_skew = imbalance(n) @assert abs(prev_skew) == 1 if prev_skew == dir double_rotate!(child(n, dir), dir) else rotate!(n, dir) end end end

Удаление записи

Удаление несколько сложнее вставки.

Для начала рассмотрим обычное удаление записи из двоичного дерева поиска.

Если удаляемая запись в листе — то запись просто удаляется, тут всё просто.
Если удаляемая запись в узле, у которого только один потомок — то этот потомок вместе со всем своим поддеревом ставится на место удалённого узла.
Если потомков два — то либо в левом поддереве ищется максимальный элемент, либо в правом минимальный, извлекается из дерева (по свойству дерева поиска узел с максимальным элементом гарантированно не имеет правого потомка, а с минимальным — левого, так что это удаление делается просто) и ставится на место удаляемой записи.

Заметим, что в самом начале гарантированно один из потомков рассматриваемого родителя уменьшил высоту на 1. Но после этого может нарушиться баланс дерева, поэтому от родителя удалённого узла нужно пройтись вверх, восстанавливая его. С учётом этого нужно рассмотреть варианты (красным показаны узлы, поменявшие высоту, обрабатываемый узел — родительский от красного):

Значит, до удаления он был 1 по модулю, и теперь дочерние узлы на 2 ниже материнского. Случай 1
Нулевой дисбаланс.

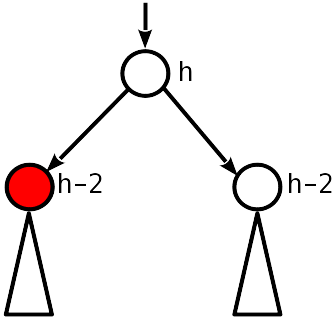
Нужно опустить родительский узел на 1 и продолжить движение вверх.

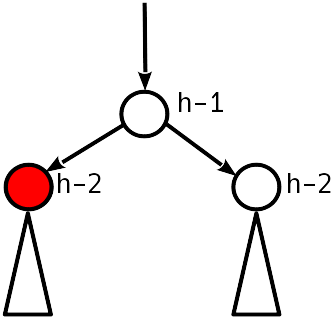
Случай 2
Дисбаланс 1 по модулю.

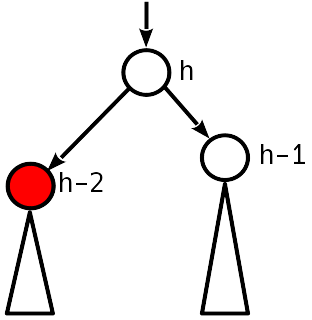
АВЛ-условие выполнено, можно остановиться.

Случай 3
Дисбаланс 2 по модулю, сестринский узел к опустившемуся имеет ненулевой дисбаланс.

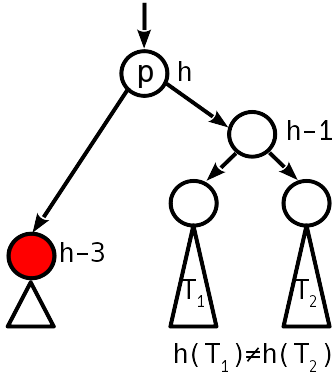
Высота поддерева при этом уменьшается, т.е. Восстанавливаем баланс простым (если T1 ниже, чем T2) или двойным (в обратном случае) поворотом, как делали при вставке. может возникнуть нарушение выше по дереву.

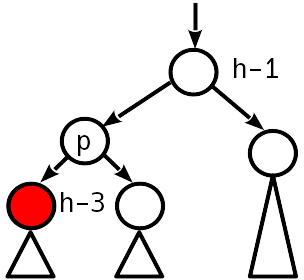
Случай 4
Дисбаланс 2 по модулю, сестринский узел имеет нулевой дисбаланс.

Простой поворот восстанавливает условие балансировки, высота поддерева при этом не меняется — останавливаем движение наверх.

Код для удаления ключа

function next_node(node::AVLNode) next = node.right if next == nothing p = node.parent next = p.parent while (next !== p) && (next.key < p.key) p, next = next, next.parent end return (next === p ? nothing : next) else while next.left != nothing next = next.left end return next end end function Base.delete!(avlt::AVLTree{K,V}, key) where {K,V} key = convert(K, key) candidate = avlt.entry.left dir = 0 while candidate.key != key dir = 2 * (key > candidate.key) - 1 candidate = child(candidate, dir) candidate == nothing && return end val = candidate.value for side in (-1, 1) if child(candidate, side) == nothing p, s = candidate.parent, child(candidate, -side) if p === p.parent insert_child!(p, s, 1) insert_child!(p, s, -1) else insert_child!(p, s, dir) fix_deletion!(p) end return end end swap = next_node(candidate) cp, sp, sr = candidate.parent, swap.parent, swap.right swap.height = candidate.height insert_child!(swap, candidate.left, -1) for side in (-1, 1) child(cp, side) === candidate && insert_child!(cp, swap, side) end if sp === candidate fix_deletion!(swap) else insert_child!(swap, candidate.right, 1) insert_child!(sp, sr, -1) fix_deletion!(sp) end return end function fix_deletion!(start::AVLNode) node = start skew = imbalance(node) while (node !== node.parent) && (abs(skew) != 1) if skew != 0 @assert abs(skew) == 2 dir = -skew ÷ 2 n = child(node, -dir) prev_skew = imbalance(n) @assert abs(prev_skew) < 2 if prev_skew == dir node = double_rotate!(child(n, dir), dir) else node = rotate!(n, dir) prev_skew != 0 || break end else node.height -= 1 end node = node.parent skew = imbalance(node) end end

Взлёт и падение АВЛ-деревьев

поворот может "сбросить" всё поддерево на уровень вниз, то в худшем случае удаление требует O(log2N) поворотов дерева — при каждом переходе на уровень вверх в fix_deletion!(). Не очень приятное свойство классических АВЛ-деревьев состоит в сложности удаления записи: т.к.

Из-за этого высота красно-чёрных деревьев составляет в худшем случае 2log2N против 1,44log2N у АВЛ-деревьев, зато удаление записи требует не более трёх простых поворотов. Из-за этой не очень хорошей асимптотики АВЛ-деревья уступили место появившимся в 1970-х красно-чёрным деревьям, у которых более слабое условие балансировки — путь от корня до самого дальнего листа не более чем вдвое превышает путь от корня до самого ближнего листа. Таким образом, поиск и вставка за счёт более высокой высоты дерева потенциально проигрывают в производительности, зато есть потенциальный выигрыш, если вставки часто перемежаются удалениями.

АВЛ наносят ответный удар

Такого пока не придумано, но в 2015 году была опубликована работа, где предложена структура, улучшающая свойства как АВЛ, так и красно-чёрных деревьев. Получается, что "идеальный" алгоритм построения двоичных деревьев поиска должен гарантировать небольшую высоту (на уровне классического АВЛ-дерева) и константное число поворотов как при добавлении, так и при удалении записи. Свойства структуры, названной "слабым АВЛ-деревом" (W(eak)AVL-деревом) формулируются таким образом: Идея лежит ближе к АВЛ деревьям, но условие баланса ослаблено, чтобы позволить более эффективное удаление записей.

Упорядоченность: для любого узла ключ в вершине левого поддерева меньше, а в вершине правого поддерева — больше, чем ключ самого узла (если потомки не являются пустыми узлами).
Возрастание ранга. Каждому узлу приписывается ранг. Ранг всех пустых узлов равен нулю, ранг листов — 1. Ранг родительского узла строго больше ранга дочернего.
Слабая АВЛ-сбалансированность: ранг узла отличается от ранга дочерних узлов не более чем на 2.

В частности, если ввести условие, что оба дочерних узла не могут отличаться от родительского по рангу на 2, то получится обычное АВЛ дерево, а ранг будет точно совпадать с высотой поддерева. Оказывается, что такая структура включает в себя свойства и классических АВЛ-деревьев, и красно-чёрных деревьев.

Оценка на высоту дерева составляет h < min(1,44log2M, 2log2N), где N — число записей в дереве, M — число вставок, по сравнению с h < 2log2N для красно-чёрных деревьев. Прелесть САВЛ-деревьев в том, что небольшое ослабление АВЛ-условия позволяет балансировать дерево при удалении записи не более чем двумя поворотами! Более того, если САВЛ-дерево строится только вставками, то оно будет идентично классическому АВЛ дереву, полученному из той же последовательности ключей.

Именно из-за этого число поворотов при удалении и становится константным. Ослабление АВЛ-условия позволяет при повороте дерева после удаления не понижать максимальный ранг узла в поддереве, что означает отсутствие необходимости балансировки выше по дереву после поворота.

Структура хранения.

Для понятности, сделаем отдельную структуру: Можно оставить структуру обычного АВЛ-дерева, только "высота" должна пониматься как "ранг".

mutable struct WAVLNode rank::UInt8 key::K value::V left::Union{Nothing, WAVLNode{K,V}} right::Union{Nothing, WAVLNode{K,V}} parent::WAVLNode{K,V} # пустой конструктор function WAVLNode{K,V}() where {K,V} node = new{K,V}() node.rank = 1 node.parent = node node.left = node.right = nothing return node end # конструктор с парой ключ-значение function WAVLNode{K,V}(key, value) where {K,V} key, value = convert(K, key), convert(V, value) node = new{K,V}() node.rank = 1 node.parent = node node.left = node.right = nothing node.key, node.value = key, value return node end end struct WAVLTree{K, V} entry::WAVLNode{K,V} WAVLTree{K,V}() where {K,V} = new{K,V}(WAVLNode{K,V}()) end function child(root::WAVLNode, side::Signed) if side == -1 root.left elseif side == 1 root.right else throw(ArgumentError("Expecting side=-1 to get the left child or side=1 to get the right child")) end end function Base.getindex(avlt::WAVLTree{K,V}, key) where {K,V} key = convert(K, key) node = avlt.entry.left while node != nothing key == node.key && return node.value node = (key < node.key ? node.left : node.right) end throw(KeyError(key)) end

Вставка записи

Едиственное отличие: если в базовом варианте дисбаланс 1 после вставки гарантированно означал, что родительский узел нужно поднять — то в ослабленном варианте нужно проверить, разница в рангах у родителя с самым высоким потомком 0 (тогда нужно поднять) или 1 (тогда делать ничего не надо). Алгоритм практически такой же, как и в обычном АВЛ-дереве. Для этого немного изменим функцию imbalance(), чтобы она возвращала и то, и другое.

wavlrank(node::Union{Nothing,WAVLNode}) = node == nothing ? 0 : Int(node.rank) function imbalance(node::WAVLNode) rr, lr = wavlrank(node.right), wavlrank(node.left) skew = rr - lr diff = node.rank - max(rr, lr) skew, diff end

При вставке, учитывая конфигурации, которые там могут возникать, он работает так же, как в обычном АВЛ-дереве, для удаления чуть-чуть иначе. Код поворотов немного меняется, чтобы не писать разные функции для поворота при вставке и удалении.

Оставшийся код для вставки

# pivot оказывается в конце на самом верху function rotate!(pivot::AVLNode, dir::Signed) dir in (-1, 1) || throw(ArgumentError("Unknown rotation direction")) p = pivot.parent g = p.parent p.height = avlheight(child(pivot, dir)) + 1 pivot.height = p.height + 1 # "перецепляем" pivot к g pivot.parent = g g.left === p && (g.left = pivot) g.right === p && (g.right = pivot) c = child(pivot, dir) # перецепляем c к p insert_child!(p, c, -dir) # перецепляем p к pivot insert_child!(pivot, p, dir) pivot end # pivot оказывается в конце на самом верху function double_rotate!(pivot::AVLNode, dir::Signed) dir in (-1, 1) || throw(ArgumentError("Unknown rotation direction")) n = pivot.parent p = n.parent g = p.parent pivot.height = n.height n.height = p.height = pivot.height - 1 # "перецепляем" pivot к g pivot.parent = g g.left === p && (g.left = pivot) g.right === p && (g.right = pivot) t2, t3 = child(pivot, -dir), child(pivot, dir) # перецепляем n к pivot и t2 к n insert_child!(n, t2, dir) insert_child!(pivot, n, -dir) # перецепляем p к pivot и t3 к p insert_child!(p, t3, -dir) insert_child!(pivot, p, dir) pivot end imbalance(node::AVLNode) = avlheight(node.right) - avlheight(node.left) function fix_insertion!(start::AVLNode) node = start.parent skew = imbalance(node) while abs(skew) == 1 node.height += 1 node = node.parent skew = imbalance(node) end @assert abs(skew) == 2 || skew == 0 if skew != 0 dir = -skew ÷ 2 n = child(node, -dir) prev_skew = imbalance(n) @assert abs(prev_skew) == 1 if prev_skew == dir double_rotate!(child(n, dir), dir) else rotate!(n, dir) end end end function Base.setindex!(avlt::AVLTree{K,V}, val, key) where {K,V} key, value = convert(K, key), convert(V, val) parent = avlt.entry.left # отдельный случай - вставка в пустое дерево if parent == nothing newnode = AVLNode{K,V}(key, value) newnode.parent = avlt.entry avlt.entry.left = avlt.entry.right = newnode return val end key_found = false while !key_found key_found = key == parent.key if key_found parent.value = value else side = (key > parent.key) * 2 - 1 next = child(parent, side) if next == nothing newnode = AVLNode{K,V}(key, value) insert_child!(parent, newnode, side) fix_insertion!(newnode) key_found = true else parent = next end end end return val end

Удаление записи

Для балансировки при обратном проходе рассматриваются следующие случаи. Поиск узла для удаления, поиск следующего и замена — полностью идентичны обычным АВЛ-деревьям.

Случай 0
Ни одно из условий баланса не нарушено, т.е.:

Дисбаланс 1, самое высокое поддерево на 1 ниже родителя
Дисбаланс 0, оба поддерева на 2 ниже родителя, при этом поддеревья не пустые.
Балансировка на этом завершается.

Случай 1
Имеем лист с рангом 2 (дисбаланс 0, поддеревья на 2 ниже и пустые).
Присваиваем узлу ранг 1 и переходим выше.

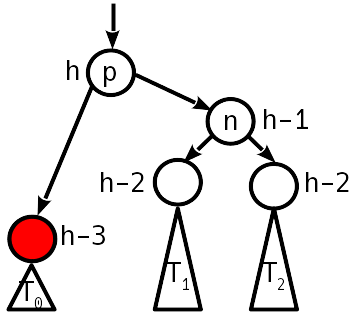
Случай 2
Дисбаланс 1, разница с максимальным поддеревом 2.

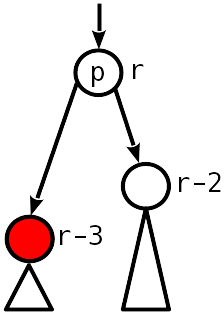
Уменьшаем у узла ранг на 1, переходим выше.

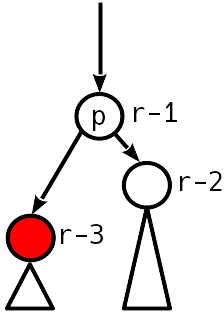
иначе слабое АВЛ условие было бы нарушено ещё до удаления), у более высокого потомка оба поддерева рангом на 2 ниже его. Случай 3
Дисбаланс 2 (разница с максимальным поддеревом автоматически 1, т.к.

Переходим выше. Спускаем на ранг ниже и сам узел, и более высокого потомка.

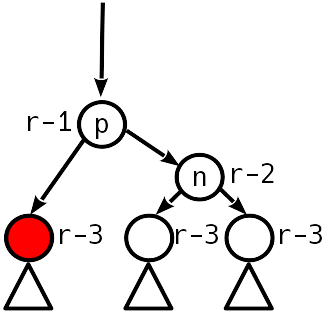
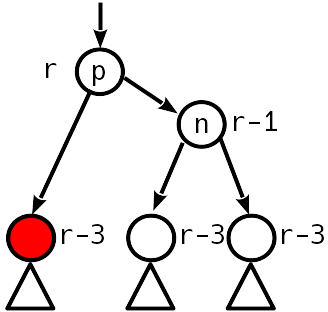
Случай 4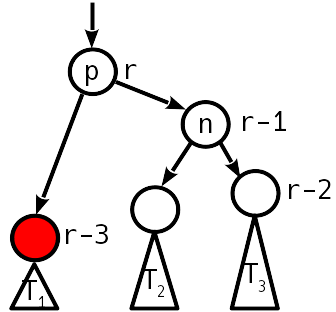

Лечится простым поворотом.

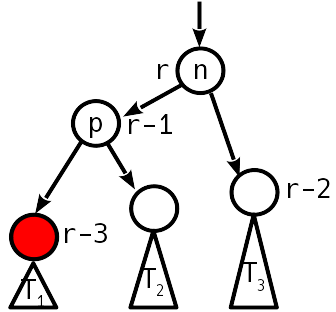
выше по дереву балансировка не требуется. Обратите внимание, что за счёт ослабленного АВЛ условия поворот можно сделать так, что всё поддерево не меняет высоту, т.е.

Единственная тонкость — если деревья T1 и T2 оба пустые, то p становится листом с рангом 2, что лечится присваиванием p в этом случае ранга 1.

Случай 5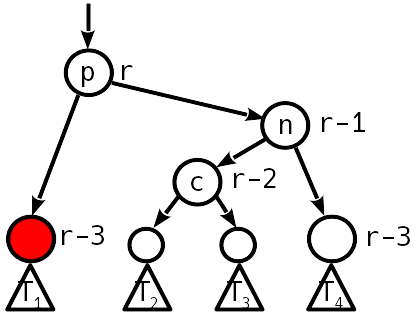

Лечится двойным поворотом.

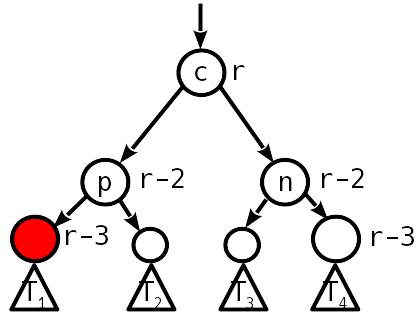
Аналогично, высота поддерева не меняется, и балансировку можно на этом заканчивать.

Код для удаления записи

function next_node(node::WAVLNode) next = node.right if next == nothing p = node.parent next = p.parent while (next !== p) && (next.key < p.key) p, next = next, next.parent end return (next === p ? nothing : next) else while next.left != nothing next = next.left end return next end end function Base.delete!(avlt::WAVLTree{K,V}, key) where {K,V} key = convert(K, key) candidate = avlt.entry.left dir = 0 while candidate.key != key dir = 2 * (key > candidate.key) - 1 candidate = child(candidate, dir) candidate == nothing && return end val = candidate.value for side in (-1, 1) if child(candidate, side) == nothing p, s = candidate.parent, child(candidate, -side) if p === p.parent insert_child!(p, s, 1) insert_child!(p, s, -1) else insert_child!(p, s, dir) fix_deletion!(p) end return end end swap = next_node(candidate) cp, sp, sr = candidate.parent, swap.parent, swap.right swap.height = candidate.height insert_child!(swap, candidate.left, -1) for side in (-1, 1) child(cp, side) === candidate && insert_child!(cp, swap, side) end if sp === candidate fix_deletion!(swap) else insert_child!(swap, candidate.right, 1) insert_child!(sp, sr, -1) fix_deletion!(sp) end return end function fix_deletion!(start::WAVLNode) node = start skew, diff = imbalance(node) while (node !== node.parent) if skew == 0 if node.right == nothing node.rank = 1 else break end elseif abs(skew) == 1 if diff == 1 break else node.rank -= 1 end else dir = -skew ÷ 2 n = child(node, -dir) prev_skew, prev_diff = imbalance(n) if prev_diff == 2 @assert prev_skew == 0 n.rank -= 1 node.rank -= 1 elseif prev_skew == dir double_rotate!(child(n, dir), dir) break else rotate!(n, dir) break end end node = node.parent skew, diff = imbalance(node) end end

Проверим в сравнении со встроенными хэш-таблицами.

julia> const wavl = WAVLTree{Int, Int}() julia> const avl = AVLTree{Int, Int}() julia> const dd = Dict{Int,Int}() julia> x = trues(1_000_000) # заполним числами и случайным образом удалим ~ половину julia> for i = 1:1_000_000; dd[i] = avl[i] = wavl[i] = i * i; end julia> for i=1:500_000 k = rand(1:1_000_000) x[k] = false delete!(avl, k) delete!(wavl, k) delete!(dd, k) end # запомнили, какие ключи не удалялись julia> const y = Int[] julia> for i in eachindex(x); if x[i] push!(y, i); end; end julia> @btime let s = 0.0; for idx in y; s += dd[idx]; end; s; end 57.626 ms (0 allocations: 0 bytes) 2.0238199367708794e17 julia> @btime let s = 0.0; for idx in y; s += wavl[idx]; end; s; end 57.796 ms (0 allocations: 0 bytes) 2.0238199367708794e17 julia> @btime let s = 0.0; for idx in y; s += avl[idx]; end; s; end 53.884 ms (0 allocations: 0 bytes) 2.0238199367708794e17

И, ожидаемо, в классическом АВЛ-дереве скорость поиска чуть выше, чем в САВЛ-дереве, за счёт лучшей сбалансированности. Итак, скорость поиска по ключу вышла примерно такая же, как во встроенных словарях.

Применение деревьев поиска

Но, на самом деле, не только. И основной вопрос — зачем это нужно?
Простейший ответ — деревья поиска нужны, чтобы искать информацию.

На основе двоичных деревьев поиска можно реализовать различные абстрактные структуры данных.

Упорядоченное множество

Также можно ввести операцию поиска n-го по величине элемента. Задача упорядоченного множества — хранить элементы так, чтобы к ним можно было доступаться в порядке возрастания или убывания. кроме перечисления, мы хотим добавлять или удалять оттуда элементы. Естественно, структуру данных рассматриваем как динамическую, т.е.

* если в узлах хранить информацию о размере поддерева

Ассоциативный массив

Во многих языках программирования, где структура включена в стандартную библиотеку, реализация сделана с помощью двоичных деревьев или хэш-таблиц. Ассоциативный массив — абстрактная структура данных, для которой основными операциями являются "найти запись по ключу", "проверить наличие ключа в массиве", "добавить пару ключ-значение", "удалить запись". В конце концов, записи можно даже просто хранить в массиве в отсортированном порядке. Языки семейства Лисп поддерживают ассоциативные списки.

* амортизированная стоимость операции
** само удаление делается за O(1), но ключ ещё нужно найти...

Очередь с приоритетами

Извлекаются записи не в порядке поступления, а в порядке приоритета. Это такая структура данных, где хранятся записи в виде пар "приоритет — данные". Часто такие очереди реализуются при помощи двоичной кучи. Основные операции — посмотреть элемент с максимальным (или минимальным) приоритетом, удалить из очереди запись со старшим приоритетом, добавить запись, изменить приоритет записи.

* если добавить в структуру указатель на максимум
** если считать, что максимум находится в конце массива

Вывод

Главная сильная черта деревьев поиска — гибкость в плане области применения, т.к. (самобалансирующиеся) Двоичные деревья поиска — неплохая структура данных для реализации ассоциативных массивов, очередей с приоритетами, и, в первую очередь, множеств, где важно упорядочение элементов. нельзя сказать, что для любой задачи деревья поиска обеспечат лучшую производительность, чем специализированные структуры.

Ссылки

"АВЛ-деревья" от nickme
Rank-Balanced Trees by Bernhard Haeupler, Siddhartha Sen, Robert E. Tarjan // ACM Transactions on Algorithms | June 2015, Vol 11(4) pdf
Goodrich M.T., Tamassia R. Algorithm Design and Applications

Теги