[Перевод] Как работает оптимизирующий компилятор

Ксюша Родионова25.11.2019

0 1 Время чтения: 23 мин.

Оптимизирующие компиляторы — основа современного ПО: они позволяют программистам писать код на понятном для них языке, затем преобразуя его в код, который сможет эффективно исполняться оборудованием. Задача оптимизирующих компиляторов заключается в том, чтобы понять, что делает написанная вами входная программ, и создать выходную программу, которая делает всё то же самое, только быстрее.

Ограничения в работе оптимизаторов варьируются в зависимости от ситуации, но задача у них одна: взять входную программу и преобразовать в выходную, которая делает то же самое, но быстрее. В этой статье мы рассмотрим некоторые из основных методик приведения (inference techniques) в оптимизирующих компиляторах: как спроектировать программу, с которой компилятору будет легко работать; какие приведения можно сделать в вашей программе и как использовать их для её уменьшения и ускорения.
Оптимизаторы программ могут выполняться где угодно: как этап большого процесса компилирования (Scala Optimizer); как отдельная программа, запускаемая после компилятора и перед исполнением (Proguard); или как часть runtime-среды, которая оптимизирует программу в ходе её исполнения (JVM JIT-компилятор).

Затем рассмотрим несколько способов представления программ, и наконец разберём алгоритмы и методики, с помощью которых можно проанализировать программы, а затем сделать их меньше и быстрее. Сначала мы рассмотрим несколько примеров оптимизаций программы-черновика, чтобы вы понимали, что обычно делают оптимизаторы и как всё это сделать вручную.

Программа-черновик

Все примеры будут приведены на Java. Этот язык очень распространён и компилируется в относительно простой ассемблер — Java Bytecode. Так мы создадим хорошую основу, благодаря которой сможем исследовать методики оптимизации компилирования на реальных, исполняемых примерах. Все описанные ниже методики применимы почти во всех остальных языках программирования.

Она содержит различную логику, регистрирует стандартный результат внутри процесса и возвращает вычисленный результат. Для начала рассмотрим программу-черновик. Сама по себе программа не имеет смысла, но будет использоваться в качестве иллюстрации того, что можно оптимизировать, сохранив существующее поведение:

static int main(int n) return total; } // https://en.wikipedia.org/wiki/Ackermann_function static int ackermann(int m, int n){ if (m == 0) return n + 1; else if (n == 0) return ackermann(m - 1, 1); else return ackermann(m - 1, ackermann(m, n - 1)); } interface Logger{ public Logger log(Object a); } static class PrintLogger implements Logger{ public PrintLogger log(Object a){ System.out.println(a); return this; } } static class ErrLogger implements Logger{ public ErrLogger log(Object a){ System.err.println(a); return this; } }

Пока что будем считать, что эта программа — всё, что у нас есть, никакие другие части кода её не вызывают. Она просто вводит данные в main, выполняет и возвращает результат. Теперь давайте оптимизировать эту программу.

Примеры оптимизаций

Приведение типов и инлайнинг

Вы могли заметить, что у переменной logger неточный тип: несмотря на метку Logger, на основании кода можно сделать вывод, что это специфический подкласс — PrintLogger:

- Logger logger = new PrintLogger(); + PrintLogger logger = new PrintLogger();

Теперь мы знаем, что logger — это PrintLogger, и знаем, что вызов logger.log может иметь единственную реализацию. Можно инлайнить:

- if (multiplied < 100) logger.logcount); + if (multiplied < 100) System.out.println(count);

Это позволит уменьшить программу за счёт удаления ненужного класса ErrLogger, который не используется, а также за счёт удаления разных методов public Logger log, поскольку мы инлайнили его в единственное место вызова.

Свёртывание констант

В ходе исполнения программы count и total изменяются, а multiplied — нет: она начинается с 0 и каждый раз умножается через multiplied = multiplied * count, оставаясь равной 0. Значит, можно заменить её во всей программе на 0:

static int main(int n){ - int count = 0, total = 0, multiplied = 0; + int count = 0, total = 0; PrintLogger logger = new PrintLogger(); while(count < n){ count += 1; - multiplied *= count; - if (multiplied < 100) System.out.println(count); + if (0 < 100) logger.log(count); total += ackermann(2, 2); - total += ackermann(multiplied, n); + total += ackermann(0, n); int d1 = ackermann(n, 1); - total += d1 * multiplied; int d2 = ackermann(n, count); if (count % 2 == 0) total += d2; } return total; }

В результате мы видим, что d1 * multiplied всегда равно 0, а значит total += d1 * multiplied ничего не делает и может быть удалено:

- total += d1 * multiplied

Удаление мёртвого кода

После свёртывания multiplied и осознания, что total += d1 * multiplied ничего не делает, можно убрать определение int d1:

- int d1 = ackermann(n, 1);

Это больше не часть программы, и поскольку ackermann является чистой функцией, удаление не повлияет на результат выполнения программы.

Аналогично, после инлайнинга logger.log сама logger больше не используется и может быть удалена:

- PrintLogger logger = new PrintLogger();

Удаление ветви

Теперь первый условный переход в нашем цикле зависит от 0 < 100. Поскольку это всегда верно, можно просто удалить условие:

- if (0 < 100) System.out.println(count); + System.out.println(count);

Любой условный переход, который всегда верен, можно инлайнить в тело условия, а для переходов, которые всегда неверны, можно удалить условие вместе с его телом.

Частичное вычисление

Теперь проанализируем три оставшихся обращения к ackermann:

total += ackermann(2, 2); total += ackermann(0, n); int d2 = ackermann(n, count);

В первом два постоянных аргумента. Функция чистая, и при предварительном вычислении ackermann(2, 2) должно быть равно 7.
Во втором обращении есть один постоянный аргумент 0 и один неизвестный n. Можно передать его в определение ackermann, и окажется, что когда m равно 0, функция всегда возвращает n + 1.
В третьем обращении оба аргумента неизвестны: n и count. Пока что оставим их на месте.

Учитывая, что обращение к ackermann определяется так:

static int ackermann(int m, int n){ if (m == 0) return n + 1; else if (n == 0) return ackermann(m - 1, 1); else return ackermann(m - 1, ackermann(m, n - 1)); }

Можно упростить его до:

- total += ackermann(2, 2); + total += 7 - total += ackermann(0, n); + total += n + 1 int d2 = ackermann(n, count);

Поздняя диспетчеризация

Определение d2 используется только в условном переходе if (count % 2 == 0). Поскольку вычисление ackermann является чистым, можно перенести этот вызов в условный переход, чтобы он не обрабатывался до тех пор, пока не будет использован:

- int d2 = ackermann(n, count); - if (count % 2 == 0) total += d2; + if (count % 2 == 0) { + int d2 = ackermann(n, count); + total += d2; + }

Это позволит избежать половины обращений к ackermann(n, count), ускорив выполнение программы.

Для сравнения, функция System.out.println не является чистой, а значит её нельзя переносить внутрь или за пределы условных переходов без изменения семантики программы.

Оптимизированный результат

Собрав все оптимизации, получим такой исходный код:

static int main(int n){ int count = 0, total = 0; while(count < n){ count += 1; System.out.println(count); total += 7; total += n + 1; if (count % 2 == 0) { total += d2; int d2 = ackermann(n, count); } } return total; } static int ackermann(int m, int n){ if (m == 0) return n + 1; else if (n == 0) return ackermann(m - 1, 1); else return ackermann(m - 1, ackermann(m, n - 1)); }

Хотя мы оптимизировали вручную, всё это можно сделать автоматически. Ниже приведён декомпилированный результат оптимизатора прототипа, который я написал для JVM-программ:

static int main(int var0) { new Demo.PrintLogger(); int var1 = 0; int var3; for(int var2 = 0; var2 < var0; var2 = var3) { System.out.println(var3 = 1 + var2); int var10000 = var3 % 2; int var7 = var1 + 7 + var0 + 1; var1 = var10000 == 0 ? var7 + ackermann(var0, var3) : var7; } return var1; } static int ackermann__I__TI1__I(int var0) { if (var0 == 0) return 2; else return ackermann(var0 - 1, var0 == 0 ? 1 : ackermann__I__TI1__I(var0 - 1);); } static int ackermann(int var0, int var1) { if (var0 == 0) return var1 + 1; else return var1 == 0 ? ackermann__I__TI1__I(var0 - 1) : ackermann(var0 - 1, ackermann(var0, var1 - 1)); } static class PrintLogger implements Demo.Logger {} interface Logger {}

Декомпилированный код чуть отличается от вручную оптимизированной версии. Кое-что компилятор не смог оптимизировать (например, неиспользуемый вызов new PrintLogger), а что-то сделано немного иначе (например, разделены ackermann и ackermann__I__TI1__I). Но в остальном автоматический оптимизатор сделал всё то же самое, что и я, используя заложенную в него логику.

Возникает вопрос: как?

Промежуточные представления

Если вы попробуете создать собственный оптимизатор, то первый же возникший вопрос будет, пожалуй, самым важным: что такое «программа»?

Вы точно исполняли их в виде скомпилированных бинарников, возможно, даже отлаживали бинарники. Несомненно, вы привыкли писать и изменять программы в виде исходного кода. Вы могли сталкиваться с программами в виде синтаксического дерева, трёхадресного кода, A-Normal, передачи продолжения (Continuation Passing Style) или Single Static Assignment.

Здесь мы обсудим самые важные способы представления «программы» внутри оптимизатора. Существует целый зоопарк разных представлений программ.

Исходный код

static int ackermann(int m, int n){ if (m == 0) return n + 1; else if (n == 0) return ackermann(m - 1, 1); else return ackermann(m - 1, ackermann(m, n - 1)); }

Некомпилированный исходный код тоже является представлением вашей программы. Он относительно компактен, удобен для чтения человеком, но у него два недостатка:

Исходный код содержит все подробности наименований и форматирования, которые важны для программиста, но бесполезны для компьютера.
Ошибочных программ в виде исходного кода гораздо больше, чем корректных, и при оптимизации нужно удостовериться, что ваша программа из корректного входного исходного кода преобразуется в корректный выходный исходный код.

Эти факторы затрудняют оптимизатору работу с программой в виде исходного кода. Да, вы можете преобразовывать такую программу, например, с помощью регулярных выражений выявляя и заменяя паттерны. Однако первый из двух факторов затрудняет надёжное выявление паттернов обилием посторонних подробностей. А второй фактор сильно повышает вероятность запутаться и получить некорректную результирующую программу.

Однако использовать исходный код в качестве первичной модели автоматизированного оптимизатора нельзя. Эти ограничения приемлемы для преобразователей программ, которые исполняются под надзором человека, например, когда можно использовать Codemod для рефакторинга и преобразования кодовой базы.

Абстрактные синтаксические деревья

static int ackermann(int m, int n){ if (m == 0) return n + 1; else if (n == 0) return ackermann(m - 1, 1); else return ackermann(m - 1, ackermann(m, n - 1)); } IfElse( cond = BinOp(Ident("m"), "=", Literal(0)), then = Return(BinOp(Ident("n"), "+", Literal(1)), else = IfElse( cond = BinOp(Ident("n"), "=", Literal(0)), then = Return(Call("ackermann", BinOp(Ident("m"), "-", Literal(1)), Literal(1)), else = Return( Call( "ackermann", BinOp(Ident("m"), "-", Literal(1)), Call("ackermann", Ident("m"), BinOp(Ident("n"), "-", Literal(1))) ) ) ) )

Они расположены на следующей ступени лестницы абстракции по сравнению с исходным кодом. Абстрактные синтаксические деревья (AST) — другой распространённый промежуточный формат. Обычно AST отбрасывают всё форматирование исходного кода, отступы и комментарии, но сохраняют имена локальных переменных, которые отбрасываются в более абстрактных представлениях.

Например, следующие два фрагмента кода семантически идентичны; они различаются только именами локальных переменных, но всё ещё имеют разные AST: Как и исходный код, AST страдают от возможности кодирования ненужной информации, которая не влияет на фактическую семантику программы.

static int ackermannA(int m, int n){ int p = n; int q = m; if (q == 0) return p + 1; else if (p == 0) return ackermannA(q - 1, 1); else return ackermannA(q - 1, ackermannA(q, p - 1)); } Block( Assign("p", Ident("n")), Assign("q", Ident("m")), IfElse( cond = BinOp(Ident("q"), "==", Literal(0)), then = Return(BinOp(Ident("p"), "+", Literal(1)), else = IfElse( cond = BinOp(Ident("p"), "==", Literal(0)), then = Return(Call("ackermann", BinOp(Ident("q"), "-", Literal(1)), Literal(1)), else = Return( Call( "ackermann", BinOp(Ident("q"), "-", Literal(1)), Call("ackermann", Ident("q"), BinOp(Ident("p"), "-", Literal(1))) ) ) ) ) ) static int ackermannB(int m, int n){ int r = n; int s = m; if (s == 0) return r + 1; else if (r == 0) return ackermannB(s - 1, 1); else return ackermannB(s - 1, ackermannB(s, r - 1)); } Block( Assign("r", Ident("n")), Assign("s", Ident("m")), IfElse( cond = BinOp(Ident("s"), "==", Literal(0)), then = Return(BinOp(Ident("r"), "+", Literal(1)), else = IfElse( cond = BinOp(Ident("r"), "==", Literal(0)), then = Return(Call("ackermann", BinOp(Ident("s"), "-", Literal(1)), Literal(1)), else = Return( Call( "ackermann", BinOp(Ident("s"), "-", Literal(1)), Call("ackermann", Ident("s"), BinOp(Ident("r"), "-", Literal(1))) ) ) ) ) )

Ключевой момент в том, что хотя AST имеют структуру деревьев, они содержат узлы, которые семантически ведут себя не как деревья: значения Ident("r") и Ident("s") определяются не содержимым их поддеревьев, а вышерасположенными узлами Assign("r", ...) и Assign("s", ...). По сути, между Ident’ами и Assign’ами есть дополнительные семантические связи, которые столь же важны, как и ребра в древовидной структуре AST:

Эти связи формируют обобщённую графовую структуру, включающую циклы при наличии рекурсивных определений функций.

Байткод

Поскольку в качестве основного языка мы выбрали Java, скомпилированные программы сохраняются в виде Java—байткода в файлах .class.

Вспомним нашу функцию ackermann:

static int ackermann(int m, int n){ if (m == 0) return n + 1; else if (n == 0) return ackermann(m - 1, 1); else return ackermann(m - 1, ackermann(m, n - 1)); }

Она компилируется в такой байткод:

0: iload_0 1: ifne 8 4: iload_1 5: iconst_1 6: iadd 7: ireturn 8: iload_1 9: ifne 20 12: iload_0 13: iconst_1 14: isub 15: iconst_1 16: invokestatic ackermann:(II)I 19: ireturn 20: iload_0 21: iconst_1 22: isub 23: iload_0 24: iload_1 25: iconst_1 26: isub 27: invokestatic ackermann:(II)I 30: invokestatic ackermann:(II)I 33: ireturn

Виртуальная машина Java (JVM), которая выполняет Java—байткод, представляет собой машину с комбинацией стека и регистров: есть стек операндов (STACK), в котором происходит оперирование значениями, и массив локальных переменных (LOCALS), в котором эти значения могут храниться. Функция начинается с N параметров в первых N слотах локальных переменных. По мере исполнения функция перемещает данные в стек, оперирует ими, кладёт обратно в переменные, вызывая return для возврата значения вызывающему из стека операндов.

Если аннотировать приведённый выше байткод для представления значений, которые перемещаются между стеком и таблицей локальных переменных, то это будет выглядеть так:

BYTECODE LOCALS STACK |a0|a1| | 0: iload_0 |a0|a1| |a0| 1: ifne 8 |a0|a1| | 4: iload_1 |a0|a1| |a1| 5: iconst_1 |a0|a1| |a1| 1| 6: iadd |a0|a1| |v1| 7: ireturn |a0|a1| | 8: iload_1 |a0|a1| |a1| 9: ifne 20 |a0|a1| | 12: iload_0 |a0|a1| |a0| 13: iconst_1 |a0|a1| |a0| 1| 14: isub |a0|a1| |v2| 15: iconst_1 |a0|a1| |v2| 1| 16: invokestatic ackermann:(II)I |a0|a1| |v3| 19: ireturn |a0|a1| | 20: iload_0 |a0|a1| |a0| 21: iconst_1 |a0|a1| |a0| 1| 22: isub |a0|a1| |v4| 23: iload_0 |a0|a1| |v4|a0| 24: iload_1 |a0|a1| |v4|a0|a1| 25: iconst_1 |a0|a1| |v4|a0|a1| 1| 26: isub |a0|a1| |v4|a0|v5| 27: invokestatic ackermann:(II)I |a0|a1| |v4|v6| 30: invokestatic ackermann:(II)I |a0|a1| |v7| 33: ireturn |a0|a1| |

Здесь я с помощью a0 и a1 представил аргументы функции, которые в самом начале функции хранятся в таблице LOCALS. 1 представляет константы, загруженные через iconst_1, а с v1 до v7 — вычисленные промежуточные значения. Здесь три инструкции ireturn, возвращающие v1, v3 и v7. Эта функция не определяет другие локальные переменные, поэтому массив LOCALS хранит только входные аргументы.

Так они выглядят в байткоде: Выше мы видели два варианта нашей функции — ackermannA и ackermannB.

BYTECODE LOCALS STACK |a0|a1| | 0: iload_1 |a0|a1| |a1| 1: istore_2 |a0|a1|a1| | 2: iload_0 |a0|a1|a1| |a0| 3: istore_3 |a0|a1|a1|a0| | 4: iload_3 |a0|a1|a1|a0| |a0| 5: ifne 12 |a0|a1|a1|a0| | 8: iload_2 |a0|a1|a1|a0| |a1| 9: iconst_1 |a0|a1|a1|a0| |a1| 1| 10: iadd |a0|a1|a1|a0| |v1| 11: ireturn |a0|a1|a1|a0| | 12: iload_2 |a0|a1|a1|a0| |a1| 13: ifne 24 |a0|a1|a1|a0| | 16: iload_3 |a0|a1|a1|a0| |a0| 17: iconst_1 |a0|a1|a1|a0| |a0| 1| 18: isub |a0|a1|a1|a0| |v2| 19: iconst_1 |a0|a1|a1|a0| |v2| 1| 20: invokestatic ackermannA:(II)I |a0|a1|a1|a0| |v3| 23: ireturn |a0|a1|a1|a0| | 24: iload_3 |a0|a1|a1|a0| |a0| 25: iconst_1 |a0|a1|a1|a0| |a0| 1| 26: isub |a0|a1|a1|a0| |v4| 27: iload_3 |a0|a1|a1|a0| |v4|a0| 28: iload_2 |a0|a1|a1|a0| |v4|a0|a1| 29: iconst_1 |a0|a1|a1|a0| |v4|a0|a1| 1| 30: isub |a0|a1|a1|a0| |v4|a0|v5| 31: invokestatic ackermannA:(II)I |a0|a1|a1|a0| |v4|v6| 34: invokestatic ackermannA:(II)I |a0|a1|a1|a0| |v7| 37: ireturn |a0|a1|a1|a0| |

Поскольку исходный код берёт два аргумента и кладёт их в локальные переменные, то у байткода есть соответствующие инструкции загрузить значения аргументов из LOCAL-индексов 0 и 1 и сохранить их под индексами 2 и 3. Однако байткод не интересуют имена ваших локальных переменных: он работает с ними исключительно как с индексами в массиве LOCALS. Поэтому у ackermannA и ackermannB будут идентичные байткоды. Это логично, ведь они семантически эквивалентны!

Нам всё ещё важно, как значения перемещаются по LOCALS и STACK, хотя они и не влияют на фактическое поведение программы. Однако ackermannA и ackermannB компилируются не в тот же байткод, что и исходная ackermann: хотя байткод абстрагируется от имён локальных переменных, он всё же не полностью абстрагируется от загрузок и сохранений в/из этих переменных.

Помимо отсутствия абстрагирования от загрузок/сохранений, у байткода есть другой недостаток: как и большинство линейных ассемблеров, он очень сильно оптимизирован с точки зрения компактности, и может быть очень трудно модифицировать его, когда речь заходит об оптимизациях.

Чтобы было понятнее, давайте рассмотрим байткод исходной функции ackermann:

Сделаем черновое изменение: пусть вызов функции 30: invokestatic ackermann:(II)I не использует свой первый аргумент. И тогда этот вызов можно заменить эквивалентным вызовом 30: invokestatic ackermann2:(I)I, который берёт лишь один аргумент. Это распространённая оптимизация, которая позволяет с помощью «удаления мёртвого кода» выкинуть любой код, использующийся для вычисления первого аргумента 30: invokestatic ackermann:(II)I.

Вернёмся от инструкции 30 к 22, а от 22 к 21 и 20. Чтобы это сделать, нам нужно не только заменить инструкцию 30, но также нужно просмотреть список инструкций и понять, где вычисляется первый аргумент (v4 в STACK), и тоже его удалить. Финальный вариант:

BYTECODE LOCALS STACK |a0|a1| | 0: iload_0 |a0|a1| |a0| 1: ifne 8 |a0|a1| | 4: iload_1 |a0|a1| |a1| 5: iconst_1 |a0|a1| |a1| 1| 6: iadd |a0|a1| |v1| 7: ireturn |a0|a1| | 8: iload_1 |a0|a1| |a1| 9: ifne 20 |a0|a1| | 12: iload_0 |a0|a1| |a0| 13: iconst_1 |a0|a1| |a0| 1| 14: isub |a0|a1| |v2| 15: iconst_1 |a0|a1| |v2| 1| 16: invokestatic ackermann:(II)I |a0|a1| |v3| 19: ireturn |a0|a1| | - 20: iload_0 |a0|a1| | - 21: iconst_1 |a0|a1| | - 22: isub |a0|a1| | 23: iload_0 |a0|a1| |a0| 24: iload_1 |a0|a1| |a0|a1| 25: iconst_1 |a0|a1| |a0|a1| 1| 26: isub |a0|a1| |a0|v5| 27: invokestatic ackermann:(II)I |a0|a1| |v6| - 30: invokestatic ackermann:(II)I |a0|a1| |v7| + 30: invokestatic ackermann2:(I)I |a0|a1| |v7| 33: ireturn |a0|a1| |

Мы ещё можем сделать такое несложное изменение в простой функции ackermann. Но в больших функциях, используемых в реальных проектах, будет гораздо труднее делать многочисленные, взаимосвязанные изменения. В целом, любое маленькое семантическое изменение вашей программы может потребовать многочисленных изменений по всему байткоду.

Эти значения передаются между LOCALS и STACK по принципу графа: от инструкции, вычисляющей значение, в место его дальнейшего использования. Вы могли заметить, что описанное выше изменение мы вносили, анализируя значения в LOCALS и STACK: смотрели, как v4 передаётся в инструкцию 30 из инструкции 22, а 22 берёт данные в a0 и 1, которые поступают из инструкций 21 и 20.

Так почему бы нам не начать работать напрямую с графом? Как и пары Ident/Assign в наших AST, значения, которые передаются между LOCALS и STACK, формируют граф между точками вычислений значений и точками их использования.

Графы потоков данных

Графы потоков данных — это следующий уровень абстракции после байткода. Если расширить наше синтаксическое дерево связями Ident/Assign, или если мы отследим, как байткод перемещает значения между LOCALS и STACK, то сможем построить граф. Для функции ackermann он выглядит так:

При анализе байткода часто приходится абстрактно интерпретировать LOCALS и STACK, чтобы понять, как движутся значения; анализ AST подразумевает отслеживание дерева и работу с символьной таблицей, содержащей связи Assign/Ident; а анализ графов потоков данных часто представляет собой прямое отслеживание переходов — чистая идея «перемещения значения», без шелухи представления программы. В отличие от AST или стеко-регистрового байткода Java, графы потоков данных не используют концепцию «локальная переменная»: вместо этого граф содержит прямые связи между каждым значением и местом его использования.

Также графами легче манипулировать, чем линейным байткодом: замена узла с вызовом ackermann на вызов ackermann2 и отброс одного из аргументов — это всего лишь изменение узла графа (помечен зелёным) и удаление одной из входных связей вместе с транзитными связями узлами (помечены красным):

Как видите, небольшое изменение в программе (замена ackermann(int n, int m) на ackermann2(int m)) превращается в относительно локализованное изменение в графе потоков данных.

В целом, работать с графами гораздо легче, чем с линейным байткодом или AST: их просто анализировать и менять.

Также я опустил ряд подробностей о преобразовании графов, например, о добавлении и удалении связей, прямых и обратных переходах, переходах горизонтальных и вертикальных (по ширине и глубине), и т. В этом описании графов нет многих подробностей: кроме фактического физического представления графа существует много других способов моделирования состояния и управления потоком, работа с которыми сложнее и выходит за рамки статьи. Если вы изучали алгоритмы, то всё это вам должно быть знакомо. д.

Это сама по себе интересная задача, но оставляем её вам для самостоятельной проработки. Наконец, мы опустили алгоритмы преобразования из линейного байткода в граф, а затем из графа обратно в байткод.

Анализ

После того, как мы получили представление программы, нужно её проанализировать: выяснить какие-то факты, которые позволят вам преобразовать программу без изменения её поведения. Многие рассмотренные выше оптимизации основаны именно на анализе программы:

Свёртывание констант: результатом работы выражения является известное постоянное значение? Вычисление выражения является чистым?
Приведение типов и инлайнинг: тип вызова метода является типом с единственной реализацией вызываемого метода?
Удаление ветвей: является булево условное выражение постоянным?
Удаление мёртвого кода: является результат компиляции «живым»? То есть он как-то влияет на результат работы программы? Вычисление чистое?
Поздняя диспетчеризация: вычисление чистое, то есть его можно перенести на другое время?

Чем больше фактов мы знаем о программе, и чем они специфичнее, тем агрессивнее мы можем преобразовать программу, чтобы оптимизировать её без изменения семантики. В этой статье мы обсудим приведение типов, константы, жизнеспособность и доступность, а анализ чистоты будет вашим самостоятельным заданием.

Анализ в оптимизаторе выполняется очень похоже на приведение типов при фронтендной проверке типов компилятором. Типы, константы, чистота, жизнеспособность — это некоторые из самых распространённых фактов, которые оптимизатор захочет узнать о вашей программе.

Структура приведений (Inference Lattice)

Для начала давайте решим, как должны работать приводимые типы и константы. По сути, «тип» отражает какое-то наше знание о значении:

Оно является Integer? String? Array[Float]? PrintLogger?
Это CharSequence? То есть значение может быть String, а может быть и чем-то вроде StringBuilder?
Или это Any, то есть мы не знаем, что это за значение?

Потенциальные типы значения в вашей программе могут быть представлены в виде такой структуры:

Поскольку у нас есть только одна строка "hello", её можно назвать одиночным типом (Singleton Type) — синглтоном. Приведение постоянного значения очень похоже на приведение типов: в некотором смысле, постоянное строковое значение "hello" является подтипом String, так же как String является подтипом CharSequence. Расширим нашу структуру синглтонами:

Чем ниже спускаемся, тем больше узнаём. Чем выше мы поднимаемся по структуре типа, присвоенного значению, тем меньше мы о нём знаем. Если мы знаем, что значение равно 0, или 1, или 2, то можно сделать вывод, что это Integer. Если мы знаем, что значение относится к одному из двух типов, например, String или StringBuilder, тогда можем консервативно предположить, что оно относится к ближайшему вышестоящему типу: CharSequence.

Можно создать ещё более гранулированную структуру, например, разделив чётные и нечётные числа:

Вам решать, насколько подробно вы будете анализировать. Чем гранулированней структура, тем точнее ваш анализ, но при этом на него уйдёт больше времени.

Приведение count

Посмотрим на упрощённую версию программы main:

static int main(int n){ int count = 0, multiplied = 0; while(count < n){ if (multiplied < 100) logger.log(count); count += 1; multiplied *= count; } return ...; }

Мы убрали разные обращения к ackermann, оставив использование только count, multiplied и logger. Так выглядит граф потоков данных:

Затем поток управления сместился в block1, где мы проверяем, выполняется ли условие count < n: если да, то идём в block3 и return, иначе идём в block2, который инкрементирует count на 1 и сохраняет результат в count, возвращая управление в block1 для повтора проверки. Мы видим, что count инициализирован равным 0 в block0. Этот цикл работает до тех пор, пока < не возвратит false, тогда мы идём в block3 и завершаем программу.

Как это проанализировать?

Начинаем с block0. Нам известно, что count = 0.
Идём в block1, мы не знаем, чему равно n (это вводимый параметр, он может быть любым числом Integer), а значит мы не знаем, куда пойдёт if. Придётся рассмотреть block2 и block3.
Игнорируем block3, поскольку это тривиально, и идём в block1b, который либо переносит напрямую в block2, либо не напрямую, сначала зажурналировав данные в block1c. Мы видим, что block2 берёт count, увеличивает его на 1 и кладёт значение обратно в count.
Мы знаем, что count может быть равен 0 или 1: смотрим на созданную выше структуру и приводим count к Integer.
Следующий круг: идём через block1 и приводим n и count к Integer.
Снова идём в block2, теперь count изменён на Integer + 1 -> Integer. Мы уже знаем, что count является Integer, поэтому можем завершить анализ.

Приведение multiplied

Рассмотрим поблочно другой граф потоков данных, относящийся к multiplied:

Начинаем в block0. Мы знаем, что multiplied присвоено значение 0.
Переходим в block1, в котором есть условный переход, который мы не смогли раньше удалить. Переходим в block2 и block3 (здесь всё просто).
В block2 обнаруживаем, что мы умножили block2 (равный 0) на count (который ранее определили как Integer). Поскольку 0 * Integer -> 0, можно оставить multiplied приведённым к 0.
Снова проходим через block1 и block2. multiplied всё ещё приведён к 0, поэтому можно прекратить анализ.

Поскольку multiplied приведён к 0, мы знаем, что:

multiplied < 100 можно привести к true.
if (multiplied < 100) logger.log(count); можно упростить до logger.log(count).
Можно убрать все вычисления, которые завершаются в multiplied, потому что мы уже знаем, что конечный результат всегда равен 0.

Эти изменения помечены красным:

Получается такой граф потоков данных:

Сериализуем его в байткод и получаем программу:

static int main(int n){ int count = 0; while(count < n){ logger.log(count); count += 1; } return ...; }

Смоделировав программу в виде подходящей структуры данных, нам хватает простых переходов по графу, чтобы упростить запутанный, неэффективный код, превратив его в маленький эффективный цикл.

В целом, приведения позволяют делать новые приведения, а одни оптимизации открывают дорогу новым. Приведение multiplied -> 0 может применяться и в других оптимизациях, например, при частичном вычислении. Основная трудность в проектировании оптимизатора программ заключается в том, чтобы он эффективно использовал этот каскад возможностей по приведению и оптимизациям.

Мы рассмотрели: В этом разделе я показал, как работает приведение в графе потоков данных.

Как можно определить структуру приведений для представления наших знаний о каждом значении в программе.
Как выглядит граф потоков данных для синтетических программ.
Как идти по графу потоков данных для выполнения приведений каждого значения в программе.
Как можно использовать эти приведения для выполнения оптимизаций: удаления ветвей или частичных вычислений по мере возможности.

В данном случае мы смогли проанализировать сначала count, а затем multiplied. Это стало возможным потому, что multiplied зависит от count, но count не зависит от multiplied. При взаимной зависимости пришлось бы анализировать переменные вместе, в ходе одного прохода по графу.

В целом, графы потоков данных без циклов (или рекурсий) всегда можно проанализировать за один проход. Обратите внимание, что приведение — процесс итеративный: вы раз за разом проходите по циклу, пока ваши приведения не перестанут изменяться. А программы с циклами или рекурсиями потребуют нескольких итераций анализа.

Поэтому более подробная структура (например, с разделением на чётные и нечётные числа) может улучшить точность анализа, но и увеличит его длительность, поэтому придётся искать компромиссы. Сейчас нам хватило только два прохода по циклу while, но может случиться так, что анализ потребует O(глубина структуры приведений) итераций.

Такой же подход можно использовать для приведения свойств произвольных рекурсивных функций, как мы сейчас увидим.

Межпроцедурное приведение функций

Выше мы приводили значения внутри единственного тела функции, ради простоты игнорируя вызовы других функций или методов. Но большинство программ содержать много функций, вызывающих друг друга, так что при работе с реальными программами вам придётся приводить свойства не только одного выражения в функции, но и самих функций, а также приводить их взаимодействие друг с другом в графе вызовов.

Простые нерекурсивные функции

В большинстве случаев обрабатывать другие функции несложно. Посмотрите на эту программу:

static int main(int n){ return called(n, 0); } static int called(int x, int y){ return x * y; }

Граф потоков данных для этих двух функций выглядит так:

Приведём возвращаемое значение main:

Приводим main(n)
- Приводим called(n, 0)
  - Приводим x * y к x = n и y = 0
  - n * 0 равно 0
- called(n, 0) равно 0
main(n) равно 0

Когда в ходе приведения вы достигаете вызова функции, то сначала приведите вызываемого, прежде чем продолжить приведение вызывающего. Этот стек приведений может быть любой глубины и отражать стек вызовов при исполнении программы.

Мы знаем, что called(n, 0) равно 0, и можем это использовать для упрощения графа потоков данных:

Сериализуем его в код:

static int main(int n){ return 0; }

Теперь наши функции не рекурсивны: если A вызывает B, вызывает C, вызывает D, затем D возвращает своё приведение к C, B, D и A. Однако если функция A вызывает B и B вызывает A, или даже A рекурсивно вызывает A, то всё это разваливается, поскольку вызовы ничего не возвращают!

Рекурсивная факториальная функция

Рассмотрим простую рекурсивную функцию, написанную на псевдо Java:

public static Any factorial(int n) { if (n == 1) { return 1; } else { return n * factorial(n - 1); } }

Она берёт n и делает его int, но возвращаемый тип помечен как Any: объявление не соответствует возвращаемым данным. Мы видим, что factorial возвращает int (или Integer в нашей структуре). Но если перед возвращением полностью анализировать тело factorial, то мы проанализируем рекурсивный вызов factorial до завершения нашего анализа самой factorial, то есть столкнёмся с бесконечной рекурсией! Как нашему движку приведения определить это от нашего имени?

Приведение с Bottom

Добавим в нашу структуру приведений специальное значение Bottom:

Применим Bottom в графе потоков данных для factorial: Оно означает «мы ещё не знаем, что это, но вернёмся сюда позднее и заполним».

Начинаем с block0. n является неизвестным Integer, 1 является 1, тогда результат n == 1 тоже неизвестен, поэтому придётся анализировать обе ветки true и false.
С true всё понятно: return возвращает 1.
В ветке false результат n - 1 благодаря n является неизвестным Integer.
factorial — это рекурсивный вызов, поэтому пока что сделаем его Bottom.
* из n: Integer и factorial: Bottom тоже пока Bottom.
return возвращает Bottom.
Вся функция factorial возвращает 1 или Bottom, а в нашей структуре ближайшим верхнеуровневым приведением для них является 1.
Вставим 1 в качестве приведения рекурсивного вызова factorial, который ранее мы пометили как Bottom.
Integer * 1 теперь Integer.
return теперь возвращает Integer.
factorial теперь возвращает Integer или 1, а ближайшим верхнеуровневым приведением для них будет Integer.
Снова приведём рекурсивный вызов factorial, на этот раз в виде Integer. Выражение * берёт n: Integer и factorial: Integer, которые остались неизменными Integer, и теперь приведения можно завершить.

Мы смогли привести возвращаемый factorial результат к Integer, несмотря на то, что это рекурсивная функция без объявления возвращаемого типа.

С рекурсивными функциями вы можете делать для вызовов заглушки из Bottom, когда впервые с ними сталкиваетесь, а по завершении первого аналитического прохода замените заглушки первым приведением и передайте это изменение вверх по графу потока данных. Хотя все эти примеры надуманы, они иллюстрируют способ приведения при наличии вызовов функций.

В данном случае выражение * проанализировано трижды:

(n: Integer) * (factorial: Bottom)
(n: Integer) * (factorial: 1)
(n: Integer) * (factorial: Integer)

Как и в случае с приведением константы multiplied из цикла, для завершения приведений может потребоваться выполнить до O(глубина структуры приведений) проходов. Этот подход обобщает другие стили рекурсивных функций и позволяет приводить другие свойства, например, чистоту.

Приведение жизнеспособности и доступности

Анализ жизнеспособности и доступности — это пара оптимизаций, которые относятся к категории «удаление мёртвого кода». При этом анализе мы ищем код, значения из которого влияют на финальный результат («живой код»), и код, который может быть достигнут потоком управления программы («доступный код»). Весь остальной код можно удалить.

Давайте рассмотрим другую упрощённую версию исходной функции main:

static int main(int n){ int count = 0, total = 0, multiplied = 0; while(count < n){ if (multiplied > 100) count += 1; count += 1; multiplied *= 2; total += 1; } return count; }

В отличие от предыдущих версий, здесь мы поменяли условный переход в if (multiplied > 100) и заменили multiplied *= count на multiplied *= 2. Так мы упростили графы программы без потери обобщённости.

Обратные проходы для оценки жизнеспособности кода

Есть две проблемы, которые нужно обнаружить в приведённой выше программе:

multiplied > 100 никогда не бывает true, поэтому count += 1 никогда не будет выполнено («недоступно»).
total хранит некоторые вычисленные значения, но одно из них не используется («нежизнеспособно»).

В идеале, программа должна выглядеть так:

static int main(int n){ int count = 0; while(count < n){ count += 1; } return count; }

Теперь давайте посмотрим, как анализатор перепишет её автоматически.

Сначала взгляните на граф потоков данных:

Он гораздо запутаннее графов, которые мы уже видели, но всё ещё читабелен: начинаем в block0, идём в block1, если одно условие истинно, то идём в block1b, если истинно другое условие, то идём в block1c, и так далее, пока не завершаем в узле return в block3.

Убираем мёртвый и недоступный код

Можем применить такое же приведение типов и констант, как и для поиска multiplied -> 0, и модифицировать граф:

Вот что получилось:

Значит ветка false из условия block1c недоступна и может быть удалена (как и условие if): Мы видим, что условный переход в block1b (0 > 100) никогда не бывает true.

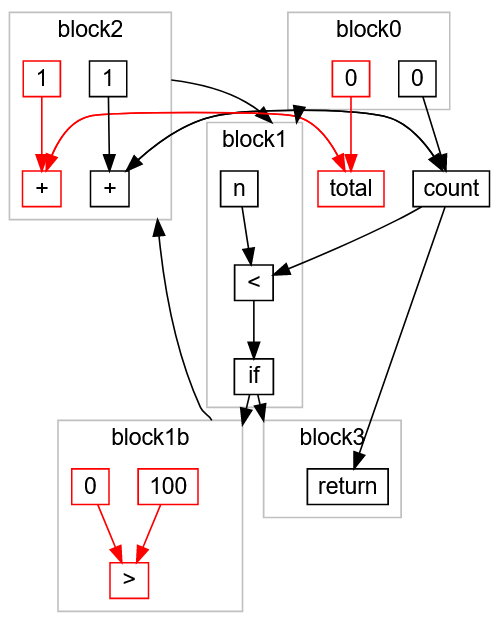
Это можно понять, пройдя по графу вверх от узла return, собирая все живые узлы и удаляя остальные: >, 100, 0 в block1b, total, 0, и + 1, передаваемый в total из block0 и block2. Наконец, мы видим «тупиковые узлы» total и >, которые что-то вычисляют, но не используются ни в одном нисходящем условном переходе, возвращении результатов или вычислении. Вот что получилось:

Сериализуем в байткод и получаем «идеальную» программу:

static int main(int n){ int count = 0; while(count < n){ count += 1; } return count; }

Заключение

В этой статье мы рассмотрели приведение программы внутри оптимизирующего компилятора:

Рассмотрели ручные оптимизации программы-черновика.
Поняли, что эти оптимизации можно делать автоматически с помощью оптимизатора.
Рассмотрели разные способы, с помощью которых оптимизирующий компилятор может моделировать вашу программу в памяти в виде промежуточного представления. В дальнейшем применяли в статье представление в виде графа потоков данных.
Рассмотрели методики приведения: «внутрипроцедурные» в рамках одной функции и «межпроцедурные» между несколькими функциями, возможно, рекурсивными.
Рассмотрели анализ на жизнеспособность и доступность: поиск частей программы, не влияющих на результат её выполнения.
Рассмотрели применение приведения и анализа для упрощения промежуточного представления, которое можно сериализовать в более простые и компактные программы.

Мы увидели, что можно превратить ручной процесс оптимизации программы в автоматизированный, применяя к простым структурам данных простые алгоритмы.

В статью многое не вошло. Это лишь небольшое введение в работу оптимизирующих компиляторов, которые делают наш код быстрее. Если хотите узнать больше, можете начать с этого:

Теги