Мозаика в ванной и диофантовы уравнения
Дело было вечером, перед сном. Чистил я зубы и устало разглядывал мозаику в ванной. Почему-то меня заинтересовал такой простой факт: если прямоугольник из клеточек 2×3 обвести с двух сторон ещё клеточками, то площадь обводки окажется такой же как площадь прямоугольника:
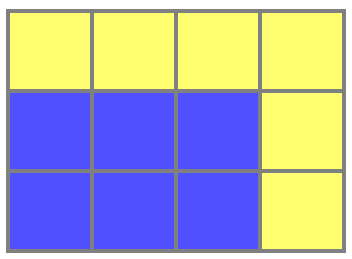
Голубых квадратиков ровно столько, сколько жёлтых. И тут меня понесло.
Я задумался, а бывают ли ещё подобные конфигурации. То есть чтобы прямоугольник обвести контуром с двух сторон, и площадь контура совпадала с площадью прямоугольника. Разумеется,
и
должны быть целыми:
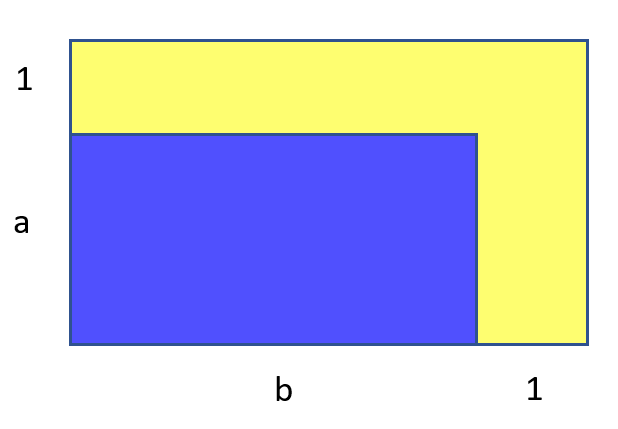
Кажется, таких случаев больше быть не должно. Площадь голубой части , а жёлтой —
. Видно, что если
или
единица, то совпадений не будет, а если увеличивать их больше
, то голубая будет явно расти быстрее. Так что такая конфигурация одна.
Скучно, сказал мозг. Надо ослабить задачу. Скажем, так:
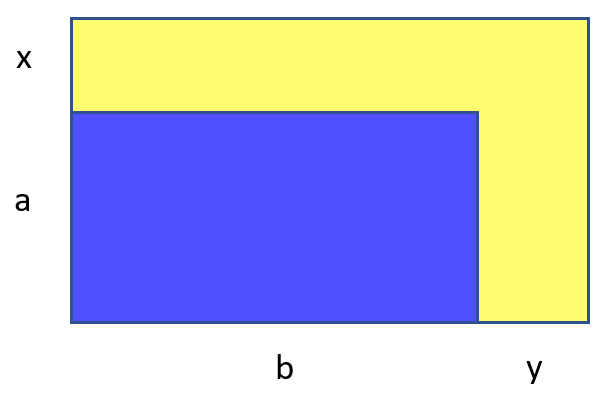
Но теперь задача слишком ослабла. По сути надо подобрать два прямоугольника с целочисленными сторонами, так что их площади отличаются ровно вдвое. И на прямоугольники ограничение только в том, чтобы один можно было засунуть в другой. Таких слишком много, тоже скучно. Давайте так:
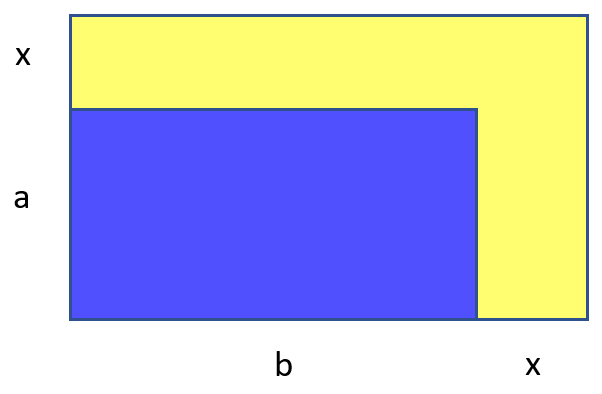
Зафиксируем ширину окантовки. Много ли таких найдётся? Хм. Выглядит интереснее. Жёлтая площадь — это , и нам хочется, чтобы она равнялась просто
. То есть нам (мне и моему мозгу, который меня в это втянул) надо решить уравнение:
Или, что то же самое:
К этому времени я закончил с зубами и принялся насыпать порошок в посудомойку. Ага, сказал мозг, неплохой челлендж. Решить надо, конечно, в целых числах, то есть это диофантово уравнение. Диофантовы уравнения мы в универе не проходили, но я вспомнил кое-что о них из популярных статей. А именно:
- Если у нас однородное уравнение, то нам повезло.
- Однородное уравнение на целых числах легко превратить в уравнение на рациональных, уменьшив число переменных на одну.
- Если методом пристального вглядывания найти какой-нибудь корень квадратного уравнения на рациональных числах, то несложно найти все остальные.
- Любая прямая с рациональными коэффициентами, проходящая через известный корень, пройдёт через ещё один корень. Крутя эту прямую, можно получить все рациональные корни.
Таким способом легко находится, например, общая формула для всех пифагоровых троек. Кстати, как и с пифагоровыми тройками, в нашей задаче любое количество кратных решений. Например, прямоугольник можно расширить окантовкой в два квадратика и так далее. Разумеется, нам интересны только некратные решения.
Смогу ли я проделать всё это в уме, подумал я, набирая увлажнитель. Алгебра без бумажки и компьютера — довольно коварная штука: перепутал плюс с минусом или забыл какой-нибудь член, и дальнейшие вычисления насмарку. Программисты знают, что делать, чтобы снизить вероятность ошибки — надо обложиться юнит-тестами. К счастью, мы знаем уже одно решение: . Будем на каждом шагу его проверять.
Пока всё идёт хорошо. Итак, у нас однородное уравнение — все члены входят во второй степени. Поделим уравнение на (случай
нас не интересует, значит, делить можно):
Делаем замену: и получаем уравнение с двумя рациональными переменными:
В нашем юнит-тесте , тест проходит. Теперь надо проводить прямую. В принципе её можно проводить как раз через точку
, но в мозгу это сложно держать. Зато методом пристального вглядывания мы легко можем найти другую точку, которая удовлетворяет уравнению:
. Это соответствует нулевой площади
и опять же как решение не очень интересно, но для проведения прямой в самый раз. Довольно просто заметить, что все прямые (кроме одной), проходящие через
, описываются явным уравнением
(да, почему-то мозг выдал греческую букву, хотя и латинские ещё не кончились). Одна недостающая прямая — это
, она тоже не очень интересна нам. Разумеется, любой рациональной точке
, где
соответствует рациональная
. Например, для точки
значение
. Подставим уравнение прямой в наше уравнение и получим:
Или
Или
Или
В голове становится сложно приводить члены, мозг отчаянно просит бумажку. Но я убаюкиваю на руках младенца, тут уж не до бумажки. Прогоним юнит-тест ():
Фуф, пока всё хорошо. Теперь у нас есть квадратное уравнение относительно , которое вообще-то должно выдать рациональный корень для любого рационального
. Как такое может быть, там же дискриминант и всё такое? Ладно, попробуем:
О-о-о, хорошо-то как, полный квадрат вышел. Эндорфин в мозг пошёл. Он, наркоман эдакий, похоже этого и добивался. Вот она магия математики: должно было выйти рациональное число и вышло. Вспоминаем формулы для корней:
Или в наших обозначениях:
— это наша опорная точка,
, это нам неинтересно. Наше решение — это
. Подставив его в
получаем ответ:
То есть надо просто перебрать все рациональные дроби в качестве , и для них мы получим все рациональные решения уравнения
(ну кроме некоторых, которые нам не очень интересны).
Разумеется, перебирать проще целые числа, а не рациональные. Спаивая младенцу препарат симетикона, я подставляю и получаю:
(Боже, мозг, зачем ты выбрал именно и
? Они так легко путаются в голове! Букв мало что ли?) В нашем юнит-тесте, если
, то подойдут
и легко убедиться, что тест проходит.
Как нам вернуться к целым числам? Вспоминаем, что мы заменили . Значит, надо принять за
любое число, кратное общему знаменателю из формул выше. В частности, подходит просто
. В итоге имеем:
Видно, что если и
не взаимно простые, то и решение будет кратно их общему делителю, поэтому нам интересны только взаимно простые
и
. Кратное решение также получится, если
окажется чётным. В самом деле пусть
. Тогда
Если поделить всё на два, то получим
Это решение симметрично первому, что вполне логично: ведь задача симметрична относительно и
. Таким образом, нам интересны взаимно простые
и
, причём
нечётно.
Удобно, что выражение для получилось таким простым. Значит, у нас есть простой способ найти все некратные решения для заданной наперёд ширины окантовки
: это такие прямоугольники
, где
любой нечётный делитель
, взаимно простой с
. Следующий прямоугольник будет для
:
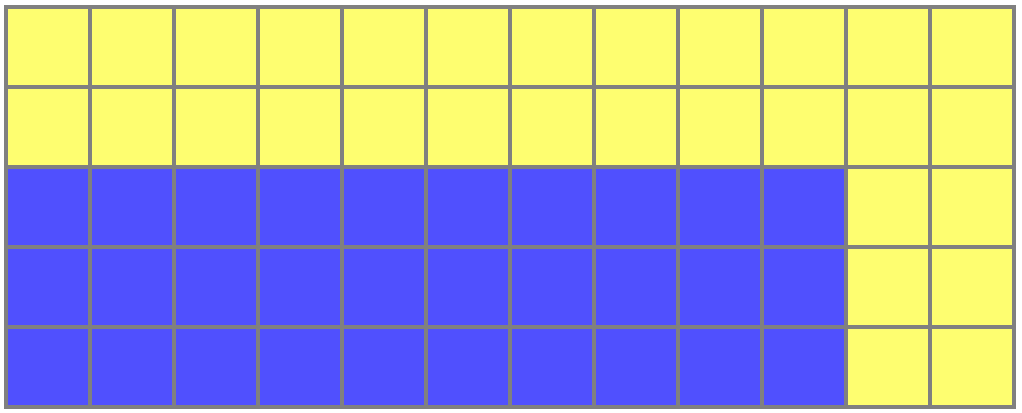
И голубая, и жёлтая часть содержат ровно по 30 клеточек!
Давайте посмотрим, какие ещё есть решения для маленьких (
и
я кое-где переставил, чтобы шли по возрастанию):
| x | n | m | площадь без окантовки | площадь с окантовкой |
|---|---|---|---|---|
| 1 | 1 | 1 | 2 × 3 = 6 | 3 × 4 = 12 |
| 2 | 1 | 2 | 3 × 10 = 30 | 5 × 12 = 60 |
| 3 | 1 | 3 | 4 × 21 = 84 | 7 × 24 = 168 |
| 3 | 3 | 1 | 5 × 12 = 60 | 8 × 15 = 120 |
| 4 | 1 | 4 | 5 × 36 = 180 | 9 × 40 = 360 |
| 5 | 1 | 5 | 6 × 55 = 330 | 11 × 60 = 660 |
| 5 | 5 | 1 | 7 × 30 = 210 | 12 × 35 = 420 |
| 6 | 1 | 6 | 7 × 78 = 546 | 13 × 84 = 1092 |
| 6 | 3 | 2 | 14 × 15 = 210 | 20 × 21 = 420 |
Насчитывая в голове эти произведения, мозг снова добился дозы эндорфина. Как красиво и чудесно делители перетекают из одного числа в другое! Взять, например, : первое делится на 6, а второе на 11. Добавляем к обоим числам пятёрку, и чудо — теперь первое делится на 11, а второе — на 6. И такие фокусы в каждой строчке! А тут и сын вроде успокоился. Одиннадцать вечера, можно и спать ложиться.
Возможно, это всё можно посчитать проще. Возможно, мои рассуждения были где-то неточными. Возможно, у этих чисел и произведений есть какое-то специальное название. Я не знаю — не искал. Мне больше вот что интересно: я один такой чушью занимаю своё сознание, или вы тоже этим страдаете наслаждаетесь? Нас вылечат?


![Фото [Перевод] Анатомия Hello World на языке C](http://orion-int.ru/wp-content/uploads/2024/04/xperevod-anatomiya-hello-world-na-yazyke-c-390x220.png.pagespeed.ic.AxnjwvMFQ9.png)




